In this paper, we consider the existence and limiting behaviour of solutions to a semilinear elliptic equation arising from confined plasma problem in dimension two\[ \begin{cases} -\Delta u=\lambda k(x)f(u) & \text{in}\ D,\\ u= c & \displaystyle\text{on}\ \partial D,\\ \displaystyle - \int_{\partial D} \frac{\partial u}{\partial \nu}\,{\rm d}s=I, \end{cases} \]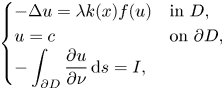
where $D\subseteq \mathbb {R}^2$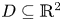 is a smooth bounded domain, $\nu$
is a smooth bounded domain, $\nu$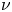 is the outward unit normal to the boundary $\partial D$
is the outward unit normal to the boundary $\partial D$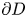 , $\lambda$
, $\lambda$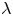 and $I$
and $I$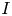 are given constants and $c$
are given constants and $c$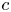 is an unknown constant. Under some assumptions on $f$
is an unknown constant. Under some assumptions on $f$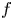 and $k$
and $k$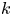 , we prove that there exists a family of solutions concentrating near strict local minimum points of $\Gamma (x)=({1}/{2})h(x,\,x)- ({1}/{8\pi })\ln k(x)$
, we prove that there exists a family of solutions concentrating near strict local minimum points of $\Gamma (x)=({1}/{2})h(x,\,x)- ({1}/{8\pi })\ln k(x)$ as $\lambda \to +\infty$
as $\lambda \to +\infty$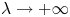 . Here $h(x,\,x)$
. Here $h(x,\,x)$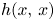 is the Robin function of $-\Delta$
is the Robin function of $-\Delta$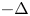 in $D$
in $D$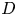 . The prescribed functions $f$
. The prescribed functions $f$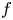 and $k$
and $k$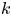 can be very general. The result is proved by regarding $k$
can be very general. The result is proved by regarding $k$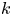 as a $measure$
as a $measure$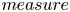 and using the vorticity method, that is, solving a maximization problem for vorticity and analysing the asymptotic behaviour of maximizers. Existence of solutions concentrating near several points is also obtained.
and using the vorticity method, that is, solving a maximization problem for vorticity and analysing the asymptotic behaviour of maximizers. Existence of solutions concentrating near several points is also obtained.