We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The unitary Cayley graph of a ring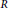 
$R$, denoted 
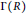$\Gamma \left( R \right)$, is the simple graph defined on all elements of 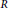$R$, and where two vertices 
$x$ and 
$y$ are adjacent if and only if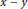 
$x\,-\,y$ is a unit in 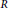$R$. The largest distance between all pairs of vertices of a graph 
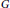$G$ is called the diameter of 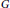$G$ and is denoted by 
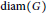$\text{diam}\left( G \right)$. It is proved that for each integer 
$n\,\ge \,1$, there exists a ring 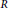$R$ such that 
$\text{diam}\left( \Gamma \left( R \right) \right)=n$. We also show that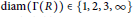 
$\text{diam}\left( \Gamma \left( R \right) \right)\in \left\{ 1,2,3,\infty \right\}$ for a ring 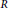$R$ with 
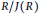${R}/{J\left( R \right)}\;$ self-injective and classify all those rings with 
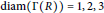$\text{diam}\left( \Gamma \left( R \right) \right)\,=\,1,\,2,\,3$, and 
$\infty$, respectively.
