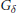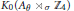For a dense ${{G}_{\delta }}$ set of real parameters $\theta $ in [0, 1] (containing the rationals) it is shown that the group ${{K}_{0}}({{A}_{\theta }}\,{{\rtimes }_{\sigma }}\,{{\mathbb{Z}}_{4}})$ is isomorphic to 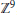${{\mathbb{Z}}^{9}}$, where 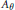${{A}_{\theta }}$ is the rotation 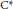${{\text{C}}^{*}}$-algebra generated by unitaries $U,\,V$ satisfying $VU\,=\,{{e}^{2\pi i\theta }}UV$ and 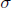$\sigma $ is the Fourier automorphism of 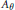${{A}_{\theta }}$ defined by 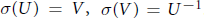$\sigma (U)\,=\,V,\,\sigma (V)\,=\,{{U}^{-1}}$. More precisely, an explicit basis for ${{K}_{0}}$ consisting of nine canonical modules is given. (A slight generalization of this result is also obtained for certain separable continuous fields of unital 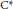${{\text{C}}^{*}}$-algebras over [0, 1].) The Connes Chern character 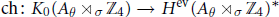$\text{ch:}\,{{K}_{0}}({{A}_{\theta }}\,{{\rtimes }_{\sigma }}\,{{\mathbb{Z}}_{4}})\,\to \,{{H}^{\text{ev}}}{{({{A}_{\theta \,}}{{\rtimes }_{\sigma }}\,{{\mathbb{Z}}_{4}})}^{*}}$ is shown to be injective for a dense 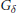${{G}_{\delta }}$ set of parameters $\theta $. The main computational tool in this paper is a group homomorphism 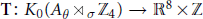$\mathbf{T}\,\text{:}\,{{K}_{0}}({{A}_{\theta }}\,{{\rtimes }_{\sigma }}\,{{\mathbb{Z}}_{4}})\,\to \,{{\mathbb{R}}^{8}}\,\times \,\mathbb{Z}$ obtained from the Connes Chern character by restricting the functionals in its codomain to a certain nine-dimensional subspace of ${{H}^{\text{ev}}}({{A}_{\theta }}\,{{\rtimes }_{\sigma }}\,{{\mathbb{Z}}_{4}})$. The range of 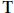$\mathbf{T}$ is fully determined for each $\theta $. (We conjecture that this subspace is all of ${{H}^{\text{ev}}}$.)

Let ${{A}_{\theta}}$ denote the rotation algebra—the universal ${{C}^{*}}$-algebra generated by unitaries $U,V$ satisfying $VU={{e}^{2\pi i\theta }}UV$, where $\theta $ is a fixed real number. Let $\sigma $ denote the Fourier automorphism of ${{A}_{\theta}}$ defined by $U\mapsto V\text{,}V\mapsto {{U}^{-1}}$, and let ${{B}_{\theta }}={{A}_{\theta }}{{\rtimes }_{\sigma }}\mathbb{Z}/4\mathbb{Z}$ denote the associated ${{C}^{*}}$-crossed product. It is shown that there is a canonical inclusion ${{\mathbb{Z}}^{9}}\hookrightarrow {{K}_{0}}({{B}_{\theta }})$ for each $\theta $ given by nine canonical modules. The unbounded trace functionals of ${{B}_{\theta }}$ (yielding the Chern characters here) are calculated to obtain the cyclic cohomology group of order zero $\text{H}{{\text{C}}^{0}}({{B}_{\theta }})$ when $\theta $ is irrational. The Chern characters of the nine modules—and more importantly, the Fourier module—are computed and shown to involve techniques from the theory of Jacobi’s theta functions. Also derived are explicit equations connecting unbounded traces across strong Morita equivalence, which turn out to be non-commutative extensions of certain theta function equations. These results provide the basis for showing that for a dense ${{\text{G}}_{\delta }}$ set of values of $\theta $ one has ${{K}_{0}}({{B}_{\theta }})\cong {{\mathbb{Z}}^{9}}$ and is generated by the nine classes constructed here.