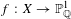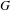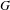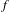We provide evidence for this conclusion: given a finite Galois cover $f:X\rightarrow \mathbb{P}_{\mathbb{Q}}^{1}$ of group $G$, almost all (in a density sense) realizations of $G$ over $\mathbb{Q}$ do not occur as specializations of $f$. We show that this holds if the number of branch points of 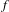$f$ is sufficiently large, under the abc-conjecture and, possibly, the lower bound predicted by the Malle conjecture for the number of Galois extensions of 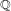$\mathbb{Q}$ of given group and bounded discriminant. This widely extends a result of Granville on the lack of 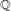$\mathbb{Q}$-rational points on quadratic twists of hyperelliptic curves over 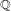$\mathbb{Q}$ with large genus, under the abc-conjecture (a diophantine reformulation of the case 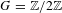$G=\mathbb{Z}/2\mathbb{Z}$ of our result). As a further evidence, we exhibit a few finite groups 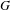$G$ for which the above conclusion holds unconditionally for almost all covers of $\mathbb{P}_{\mathbb{Q}}^{1}$ of group $G$. We also introduce a local–global principle for specializations of Galois covers 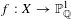$f:X\rightarrow \mathbb{P}_{\mathbb{Q}}^{1}$ and show that it often fails if 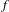$f$ has abelian Galois group and sufficiently many branch points, under the abc-conjecture. On the one hand, such a local–global conclusion underscores the ‘smallness’ of the specialization set of a Galois cover of 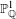$\mathbb{P}_{\mathbb{Q}}^{1}$. On the other hand, it allows to generate conditionally ‘many’ curves over 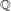$\mathbb{Q}$ failing the Hasse principle, thus generalizing a recent result of Clark and Watson devoted to the hyperelliptic case.