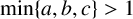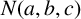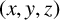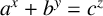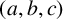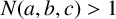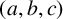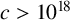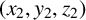Let a, b, c be fixed coprime positive integers with $\min \{ a,b,c \}>1$. Let $N(a,b,c)$ denote the number of positive integer solutions $(x,y,z)$ of the equation $a^x + b^y = c^z$. We show that if $(a,b,c)$ is a triple of distinct primes for which $N(a,b,c)>1$ and $(a,b,c)$ is not one of the six known such triples, then $c>10^{18}$, and there are exactly two solutions $(x_1, y_1, z_1)$, $(x_2, y_2, z_2)$ with 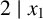$2 \mid x_1$, $2 \mid y_1$, 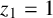$z_1=1$, 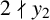$2 \nmid y_2$, 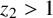$z_2>1$, and, taking 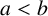$a<b$, we must have $a=2$, 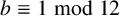$b \equiv 1 \bmod 12$, 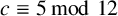$c \equiv 5\, \mod 12$, with $(a,b,c)$ satisfying further strong restrictions. These results support a conjecture put forward by Scott and Styer [‘Number of solutions to 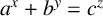$a^x + b^y = c^z$’, Publ. Math. Debrecen 88 (2016), 131–138].

Let a, b, c be fixed coprime positive integers with $\min \{a,b,c\}>1$ . We discuss the conjecture that the equation $a^{x}+b^{y}=c^{z}$ has at most one positive integer solution $(x,y,z)$ with $\min \{x,y,z\}>1$ , which is far from solved. For any odd positive integer r with $r>1$ , let $f(r)=(-1)^{(r-1)/2}$ and $2^{g(r)}\,\|\, r-(-1)^{(r-1)/2}$ . We prove that if one of the following conditions is satisfied, then the conjecture is true: (i) $c=2$ ; (ii) a, b and c are distinct primes; (iii) $a=2$ and either $f(b)\ne f(c)$ , or $f(b)=f(c)$ and $g(b)\ne g(c)$ .

Jeśmanowicz conjectured that $(x,y,z)=(2,2,2)$ is the only positive integer solution of the equation $(*)\; ((\kern1.5pt f^2-g^2)n)^x+(2fgn)^y=((\kern1.5pt f^2+g^2)n)^x$ , where n is a positive integer and f, g are positive integers such that $f>g$ , $\gcd (\kern1.5pt f,g)=1$ and $f \not \equiv g\pmod 2$ . Using Baker’s method, we prove that: (i) if $n>1$ , $f \ge 98$ and $g=1$ , then $(*)$ has no positive integer solutions $(x,y,z)$ with $x>z>y$ ; and (ii) if $n>1$ , $f=2^rs^2$ and $g=1$ , where r, s are positive integers satisfying $(**)\; 2 \nmid s$ and $s<2^{r/2}$ , then $(*)$ has no positive integer solutions $(x,y,z)$ with $y>z>x$ . Thus, Jeśmanowicz’ conjecture is true if $f=2^rs^2$ and $g=1$ , where r, s are positive integers satisfying $(**)$ .