We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Williamson’s theorem states that for any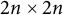 
$2n \times 2n$ real positive definite matrix A, there exists a 
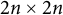$2n \times 2n$ real symplectic matrix S such that 
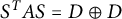$S^TAS=D \oplus D$, where D is an 
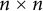$n\times n$ diagonal matrix with positive diagonal entries known as the symplectic eigenvalues of A. Let H be any 
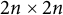$2n \times 2n$ real symmetric matrix such that the perturbed matrix 
$A+H$ is also positive definite. In this paper, we show that any symplectic matrix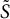 
$\tilde {S}$ diagonalizing 
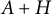$A+H$ in Williamson’s theorem is of the form 
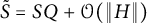$\tilde {S}=S Q+\mathcal {O}(\|H\|)$, where Q is a 
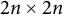$2n \times 2n$ real symplectic as well as orthogonal matrix. Moreover, Q is in symplectic block diagonal form with the block sizes given by twice the multiplicities of the symplectic eigenvalues of A. Consequently, we show that 
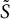$\tilde {S}$ and S can be chosen so that 
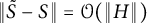$\|\tilde {S}-S\|=\mathcal {O}(\|H\|)$. Our results hold even if A has repeated symplectic eigenvalues. This generalizes the stability result of symplectic matrices for non-repeated symplectic eigenvalues given by Idel, Gaona, and Wolf [Linear Algebra Appl., 525:45–58, 2017].
