The Hamiltonian shape invariant of a domain 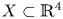 $X \subset \mathbb {R}^4$, as a subset of
$X \subset \mathbb {R}^4$, as a subset of  $\mathbb {R}^2$, describes the product Lagrangian tori which may be embedded in
$\mathbb {R}^2$, describes the product Lagrangian tori which may be embedded in 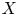 $X$. We provide necessary and sufficient conditions to determine whether or not a path in the shape invariant can lift, that is, be realized as a smooth family of embedded Lagrangian tori, when
$X$. We provide necessary and sufficient conditions to determine whether or not a path in the shape invariant can lift, that is, be realized as a smooth family of embedded Lagrangian tori, when 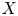 $X$ is a basic
$X$ is a basic 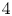 $4$-dimensional toric domain such as a ball
$4$-dimensional toric domain such as a ball  $B^4(R)$, an ellipsoid
$B^4(R)$, an ellipsoid 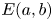 $E(a,b)$ with
$E(a,b)$ with  ${b}/{a} \in \mathbb {N}_{\geq ~2}$, or a polydisk
${b}/{a} \in \mathbb {N}_{\geq ~2}$, or a polydisk 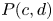 $P(c,d)$. As applications, via the path lifting, we can detect knotted embeddings of product Lagrangian tori in many toric
$P(c,d)$. As applications, via the path lifting, we can detect knotted embeddings of product Lagrangian tori in many toric  $X$. We also obtain novel obstructions to symplectic embeddings between domains that are more general than toric concave or toric convex.
$X$. We also obtain novel obstructions to symplectic embeddings between domains that are more general than toric concave or toric convex.