We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Erdős conjectured that for any set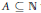 
$A\,\subseteq \,\mathbb{N}$ with positive lower asymptotic density, there are infinite sets 
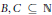$B,\,C\,\subseteq \,\mathbb{N}$ such that 
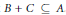$B\,+\,C\,\subseteq \,A$. We verify Erdős’ conjecture in the case where 
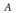$A$ has Banach density exceeding 
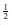$\frac{1}{2}$. As a consequence, we prove that, for 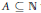$A\,\subseteq \,\mathbb{N}$ with positive Banach density (a much weaker assumption than positive lower density), we can find infinite 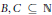$B,\,C\,\subseteq \,\mathbb{N}$ such that 
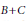$B\,+\,C$ is contained in the union of 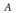$A$ and a translate of 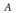$A$. Both of the aforementioned results are generalized to arbitrary countable amenable groups. We also provide a positive solution to Erdős’ conjecture for subsets of the natural numbers that are pseudorandom.
