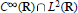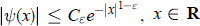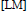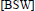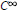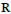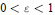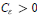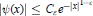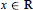1 results
Band-Limited Wavelets with Subexponential Decay
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 4 / 01 December 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 398-403
- Print publication:
- 01 December 1998
-
- Article
-
- You have access
- Export citation
-
It is well known that the compactly supported wavelets cannot belong to the class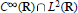
${{C}^{\infty }}\,(\text{R})\,\cap \,{{L}^{2}}\,(R)$. This is also true for wavelets with exponential decay. We show that one can construct wavelets in the class 
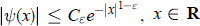${{C}^{\infty }}\,(\text{R})\,\cap \,{{L}^{2}}\,(R)$ that are “almost” of exponential decay and, moreover, they are band-limited. We do this by showing that we can adapt the construction of the Lemarié-Meyer wavelets 
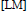$[\text{LM }\!\!]\!\!\text{ }$ that is found in 
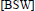$[\text{BSW}]$ so that we obtain band-limited, 
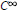${{C}^{\infty }}$-wavelets on 
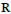$R$ that have subexponential decay, that is, for every 
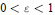$0<\varepsilon <1$, there exits 
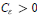${{C}_{\in }}\,>\,0$ such that 
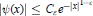$|\psi (x)|\le {{C}_{\varepsilon }}{{e}^{-|x{{|}^{1-\varepsilon }}}}$, 
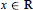$x\in \text{R}$. Moreover, all of its derivatives have also subexponential decay. The proof is constructive and uses the Gevrey classes of functions.
