We prove that any surjective isometry between unit spheres of the 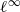 ${\ell }^{\infty } $-sum of strictly convex normed spaces can be extended to a linear isometry on the whole space, and we solve the isometric extension problem affirmatively in this case.
${\ell }^{\infty } $-sum of strictly convex normed spaces can be extended to a linear isometry on the whole space, and we solve the isometric extension problem affirmatively in this case.
 ${\ell }^{\infty } $-SUM OF STRICTLY CONVEX NORMED SPACES
${\ell }^{\infty } $-SUM OF STRICTLY CONVEX NORMED SPACES