We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper, we are concerned with the ground states of the following planar Kirchhoff-type problem:\[ -\left(1+b\displaystyle\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)\Delta u+\omega u=|u|^{p-2}u, \quad x\in\mathbb{R}^2. \]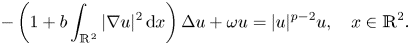where $b,\, \omega >0$
are constants, $p>2$
. Based on variational methods, regularity theory and Schwarz symmetrization, the equivalence of ground state solutions for the above problem with the minimizers for some minimization problems is obtained. In particular, a new scale technique, together with Lagrange multipliers, is delicately employed to overcome some intrinsic difficulties.
