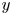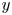This paper is concerned with the relationship of $y$-smooth integers and de Bruijn's approximation $\Lambda (x,\,y)$. Under the Riemann hypothesis, Saias proved that the count of $y$-smooth integers up to $x$, $\Psi (x,\,y)$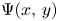, is asymptotic to $\Lambda (x,\,y)$ 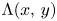when $y \ge (\log x)^{2+\varepsilon }$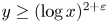. We extend the range to $y \ge (\log x)^{3/2+\varepsilon }$ 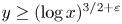by introducing a correction factor that takes into account the contributions of zeta zeros and prime powers. We use this correction term to uncover a lower order term in the asymptotics of $\Psi (x,\,y)/\Lambda (x,\,y)$. The term relates to the error term in the prime number theorem, and implies that large positive (resp. negative) values of $\sum _{n \le y} \Lambda (n)-y$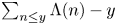 lead to large positive (resp. negative) values of $\Psi (x,\,y)-\Lambda (x,\,y)$, and vice versa. Under the Linear Independence hypothesis, we show a Chebyshev's bias in $\Psi (x,\,y)-\Lambda (x,\,y)$.

We investigate the leading digit distribution of the kth largest prime factor of n (for each fixed $k=1,2,3,\dots $ ) as well as the sum of all prime factors of n. In each case, we find that the leading digits are distributed according to Benford’s law. Moreover, Benford behavior emerges simultaneously with equidistribution in arithmetic progressions uniformly to small moduli.

Given $f\in \mathbb{Z}[t]$ of positive degree, we investigate the existence of auxiliary polynomials $g\in \mathbb{Z}[t]$ for which $f(g(t))$ factors as a product of polynomials of small relative degree. One consequence of this work shows that for any quadratic polynomial $f\in \mathbb{Z}[t]$ and any $\unicode[STIX]{x1D700}>0$, there are infinitely many $n\in \mathbb{N}$ for which the largest prime factor of $f(n)$ is no larger than $n^{\unicode[STIX]{x1D700}}$.

We investigate exponential sums over those numbers ${\leqslant}x$ all of whose prime factors are ${\leqslant}y$. We prove fairly good minor arc estimates, valid whenever $\log ^{3}x\leqslant y\leqslant x^{1/3}$. Then we prove sharp upper bounds for the $p$th moment of (possibly weighted) sums, for any real $p>2$ and $\log ^{C(p)}x\leqslant y\leqslant x$. Our proof develops an argument of Bourgain, showing that this can succeed without strong major arc information, and roughly speaking it would give sharp moment bounds and restriction estimates for any set sufficiently factorable relative to its density. By combining our bounds with major arc estimates of Drappeau, we obtain an asymptotic for the number of solutions of $a+b=c$ in $y$-smooth integers less than $x$ whenever $\log ^{C}x\leqslant y\leqslant x$. Previously this was only known assuming the generalised Riemann hypothesis. Combining them with transference machinery of Green, we prove Roth’s theorem for subsets of the $y$-smooth numbers whenever $\log ^{C}x\leqslant y\leqslant x$. This provides a deterministic set, of size ${\approx}x^{1-c}$, inside which Roth’s theorem holds.

Let R(n,θ) denote the number of representations of the natural number n as the sum of four squares, each composed only with primes not exceeding nθ/2. When θ>e−1/3 a lower bound for R(n,θ) of the expected order of magnitude is established, and when θ>365/592, it is shown that R(n,θ)>0 holds for large n. A similar result is obtained for sums of three squares. An asymptotic formula is obtained for the related problem of representing an integer as the sum of two squares and two squares composed of small primes, as above, for any fixed θ>0. This last result is the key to bound R(n,θ) from below.

Non-trivial estimates for fractional moments of smooth cubic Weyl sums are developed. Complemented by bounds for such sums of use on both the major and minor arcs in a Hardy--Littlewood dissection, these estimates are applied to derive an upper bound for the $s$th moment of the smooth cubic Weyl sum of the expected order of magnitude as soon as $s\ge 7.691$. Related arguments demonstrate that all large integers $n$ are represented as the sum of eight cubes of natural numbers, all of whose prime divisors are at most $\exp (c(\log n\log \log n)^{1/2})$, for a suitable positive number $c$. This conclusion improves a previous result of G. Harcos in which nine cubes are required. 1991 Mathematics Subject Classification: 11P05, 11L15, 11P55.

Let $\mathcal{S}$ denote the set of integers representable as a sum of two squares. Since $\mathcal{S}$ can be described as the unsifted elements of a sieving process of positive dimension, it is to be expected that $\mathcal{S}$ has many properties in common with the set of prime numbers. In this paper we exhibit “unexpected irregularities” in the distribution of sums of two squares in short intervals, a phenomenon analogous to that discovered by Maier, over a decade ago, in the distribution of prime numbers. To be precise, we show that there are infinitely many short intervals containing considerably more elements of $\mathcal{S}$ than expected, and infinitely many intervals containing considerably fewer than expected.

We investigate conditions which ensure that systems of binomial polynomials with integer coefficients are simultaneously free of large prime factors. In particular, for each positive number ε, we show that there are infinitely many strings of consecutive integers of size about n, free of prime factors exceeding nε, with the length of the strings tending to infinity with speed log log log log n.