We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We prove the existence of a family of slow-decay positive solutions of a supercritical elliptic equation with Hardy potential
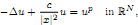
and study the stability and oscillation properties of these solutions. We also show that if the equation on ℝN has a stable slow-decay positive solution, then for any smooth compact K ⊂ ℝN a family of the exterior Dirichlet problems in ℝN \ K admits a continuum of stable slow-decay infinite-energy solutions.
