We consider the problem of finding two free export/import sets $E^+$ and $E^-$ that minimize the total cost of some export/import transportation problem (with export/import taxes $g^\pm $ ), between two densities $f^+$ and $f^-$ , plus penalization terms on $E^+$ and $E^-$ . First, we prove the existence of such optimal sets under some assumptions on $f^\pm $ and $g^\pm $ . Then we study some properties of these sets such as convexity and regularity. In particular, we show that the optimal free export (resp. import) region $E^+$ (resp. $E^-$ ) has a boundary of class $C^2$ as soon as $f^+$ (resp. $f^-$ ) is continuous and $\partial E^+$ (resp. $\partial E^-$ ) is $C^{2,1}$ provided that $f^+$ (resp. $f^-$ ) is Lipschitz.

In this paper we study spectral properties of the Dirichlet-to-Neumann map on differential forms obtained by a slight modification of the definition due to Belishev and Sharafutdinov. The resulting operator $\unicode[STIX]{x039B}$ is shown to be self-adjoint on the subspace of coclosed forms and to have purely discrete spectrum there. We investigate properties of eigenvalues of $\unicode[STIX]{x039B}$ and prove a Hersch–Payne–Schiffer type inequality relating products of those eigenvalues to eigenvalues of the Hodge Laplacian on the boundary. Moreover, non-trivial eigenvalues of $\unicode[STIX]{x039B}$ are always at least as large as eigenvalues of the Dirichlet-to-Neumann map defined by Raulot and Savo. Finally, we remark that a particular case of $p$-forms on the boundary of a $2p+2$-dimensional manifold shares many important properties with the classical Steklov eigenvalue problem on surfaces.

We prove a reverse Faber–Krahn inequality for the Cheeger constant, stating that every convex body in ℝ2 has an affine image such that the product between its Cheeger constant and the square root of its area is not larger than the same quantity for the regular triangle. An analogous result holds for centrally symmetric convex bodies with the regular triangle replaced by the square. We also prove a Mahler-type inequality for the Cheeger constant, stating that every axisymmetric convex body in ℝ2 has a linear image such that the product between its Cheeger constant and the Cheeger constant of its polar body is not larger than the same quantity for the square.

It has been shown by Kesavan (Proc. R. Soc. Edinb. A (133) (2003), 617–624) that the first eigenvalue for the Dirichlet Laplacian in a punctured ball, with the puncture having the shape of a ball, is maximum if and only if the balls are concentric. Recently, Emamizadeh and Zivari-Rezapour (Proc. Am. Math. Soc.136 (2007), 1325–1331) have tried to generalize this result to the case of the p-Laplacian but could succeed only in proving a domain monotonicity result for a weighted eigenvalue problem in which the weights need to satisfy some artificial conditions. In this paper we generalize the result of Kesavan to the case of the p-Laplacian (1 < p < ∞) without any artificial restrictions, and in the process we simplify greatly the proof, even in the case of the Laplacian. The uniqueness of the maximizing domain in the nonlinear case is still an open question.

We consider the variational problem

        inf{αλ1(Ω) + βλ2(Ω) + (1 − α − β)λ3(Ω) | Ω open in ℝn, |Ω| ≤ 1},

for α, β ∈ [0, 1], α + β ≤ 1, where λk(Ω) is the kth eigenvalue of the Dirichlet Laplacian acting in L2(Ω) and |Ω| is the Lebesgue measure of Ω. We investigate for which values of α, β every minimiser is connected.

The problem of distributing two conducting materials with a prescribed volume ratio in aball so as to minimize the first eigenvalue of an elliptic operator with Dirichletconditions is considered in two and three dimensions. The gap ε between the twoconductivities is assumed to be small (low contrast regime). The main result of the paperis to show, using asymptotic expansions with respect to ε and to small geometricperturbations of the optimal shape, that the global minimum of the first eigenvalue in lowcontrast regime is either a centered ball or the union of a centered ball and of acentered ring touching the boundary, depending on the prescribed volume ratio between thetwo materials.

In this paper we consider a model shape optimization problem. The state variable solvesan elliptic equation on a domain with one part of the boundary described as the graph of acontrol function. We prove higher regularity of the control and develop a priorierror analysis for the finite element discretization of the shape optimizationproblem under consideration. The derived a priori error estimates areillustrated on two numerical examples.

We consider the shape optimization problem \hbox{$\min\big\{\E(\Gamma)\ :\ \Gamma\in\A,\ \H^1(\Gamma)=l\\big\},$}min{ℰ(Γ):Γ ∈ 𝒜,ℋ1(Γ) = l}, where ℋ1 is the one-dimensional Hausdorffmeasure and𝒜is an admissible class of one-dimensional setsconnecting some prescribed set of points \hbox{$\D=\{D_1,\dots,D_k\}\subset\R^d$}𝒟 =  { D1,...,Dk }  ⊂ Rd. The cost functional ℰ(Γ) is theDirichlet energy of Γ defined through the Sobolev functions onΓ vanishing on the pointsDi. We analyze the existence of a solutionin both the families of connected sets and of metric graphs. At the end, several explicitexamples are discussed.

We review the optimal design of an arterial bypass graft following either a (i) boundaryoptimal control approach, or a (ii) shape optimization formulation. The main focus isquantifying and treating the uncertainty in the residual flow when the hosting artery isnot completely occluded, for which the worst-case in terms of recirculation effects isinferred to correspond to a strong orifice flow through near-complete occlusion.Aworst-case optimal control approach is applied to the steady Navier-Stokes equations in 2Dto identify an anastomosis angle and a cuffed shape that are robust with respect to apossible range of residual flows. We also consider a reduced order modelling frameworkbased on reduced basis methods in order to make the robust design problem computationallyfeasible. The results obtained in 2D are compared with simulations in a 3D geometry butwithout model reduction or the robust framework.

The least Steklov eigenvalue d1 for the biharmonic operatorin bounded domains gives a bound for the positivity preserving property for the hingedplate problem, appears as a norm of a suitable trace operator, and gives the optimalconstant to estimate the L2-norm of harmonic functions. Theseapplications suggest to address the problem of minimizing d1in suitable classes of domains. We survey the existing results and conjectures about thistopic; in particular, the existence of a convex domain of fixed measure minimizingd1 is known, although the optimal shape is still unknown. Weperform several numerical experiments which strongly suggest that the optimal planar shapeis the regular pentagon. We prove the existence of a domain minimizingd1 also among convex domains having fixed perimeter andpresent some numerical results supporting the conjecture that, among planar domains, thedisk is the minimizer.

A body moves in a rarefied medium composed of point particles at rest. The particles make elastic reflections when colliding with the body surface and do not interact with each other. 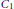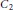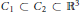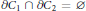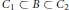We consider a generalization of Newton’s minimal resistance problem: given two bounded convex bodies ${{C}_{1}}$ and ${{C}_{2}}$ such that ${{C}_{1}}\,\subset \,{{C}_{2}}\,\subset \,{{\mathbb{R}}^{3}}$ and $\partial {{C}_{1}}\,\cap \,\partial {{C}_{2}}\,=\,\varnothing $, minimize the resistance in the class of connected bodies $B$ such that ${{C}_{1}}\,\subset \,B\,\subset \,{{C}_{2}}$. We prove that the infimum of resistance is zero; that is, there exist “almost perfectly streamlined” bodies.

We examine shape optimization problems in the context of inexact sequential quadraticprogramming. Inexactness is a consequence of using adaptive finite element methods (AFEM)to approximate the state and adjoint equations (via the dual weightedresidual method), update the boundary, and compute the geometric functional. We present anovel algorithm that equidistributes the errors due to shape optimization anddiscretization, thereby leading to coarse resolution in the early stages and fineresolution upon convergence, and thus optimizing the computational effort. We discuss theability of the algorithm to detect whether or not geometric singularities such as cornersare genuine to the problem or simply due to lack of resolution – a new paradigm inadaptivity.

In this paper we study the compact and convex setsK ⊆ Ω ⊆ ℝ2 that minimize

\begin{equation*} \int_{\Omega} \dist(\x,K) \,{\rm d}\x +\lambda_1 {\rm Vol}(K)+\lambda_2 {\rm Per}(K) \end{equation*}${\mathrm{\int }}_{\mathit{\Omega }}\mathrm{dist}\mathrm{\left(}{x}\mathit{,K}\mathrm{\right)}\mathrm{d}{x}\mathrm{+}{\mathit{\lambda }}_{\mathrm{1}}\mathrm{Vol}\mathrm{\left(}\mathit{K}\mathrm{\right)}\mathrm{+}{\mathit{\lambda }}_{\mathrm{2}}\mathrm{Per}\mathrm{\left(}\mathit{K}\mathrm{\right)}$

Dans ce travail, nous nous sommes intéressés à l’optimisation de forme des structures dont le comportement est hyperélastique incompressible et anisotrope. La fonction énergie est décomposée en une composante isotrope et une composante anisotrope. L’approche décrite dans cet article est le calcul exact de la sensibilité pour les éléments solides en utilisant un matériau à comportement hyperélastique. La résolution du problème mécanique est faite par la méthode des éléments-finis en utilisant un algorithme d’optimisation appelé SQP (Sequential Quadratic Programming). Le critère d’optimisation (fonction objectif à minimiser) est défini à partir du critère de Von Mises avec une limitation de conservation du volume. Les variables d’optimisation sont les coordonnées des points de contrôle avec une paramétrisation par les courbes de B-splines. La faisabilité de la méthode développée est validée par un exemple numérique avec une comparaison du calcul de la sensibilité par la méthode des différences finies.

Shape optimization of mechanical devices is investigated in the context of large, geometrically strongly nonlinear deformations and nonlinear hyperelastic constitutive laws. A weighted sum of the structure compliance, its weight, and its surface area are minimized. The resulting nonlinear elastic optimization problem differs significantly from classical shape optimization in linearized elasticity. Indeed, there exist different definitions for the compliance: the change in potential energy of the surface load, the stored elastic deformation energy, and the dissipation associated with the deformation. Furthermore, elastically optimal deformations are no longer unique so that one has to choose the minimizing elastic deformation for which the cost functional should be minimized, and this complicates the mathematical analysis. Additionally, along with the non-uniqueness, buckling instabilities can appear, and the compliance functional may jump as the global equilibrium deformation switches between different bluckling modes. This is associated with a possible non-existence of optimal shapes in a worst-case scenario. In this paper the sharp-interface description of shapes is relaxed via an Allen-Cahn or Modica-Mortola type phase-field model, and soft material instead of void is considered outside the actual elastic object. An existence result for optimal shapes in the phase field as well as in the sharp-interface model is established, and the model behavior for decreasing phase-field interface width is investigated in terms of Γ-convergence. Computational results are based on a nested optimization with a trust-region method as the inner minimization for the equilibrium deformation and a quasi-Newton method as the outer minimization of the actual objective functional. Furthermore, a multi-scale relaxation approach with respect to the spatial resolution and the phase-field parameter is applied. Various computational studies underline the theoretical observations.

A Bernoulli free boundary problem with geometrical constraints is studied. The domain Ω is constrained to lie in the half space determined by x1 ≥ 0 and its boundary to contain a segment of the hyperplane  {x1 = 0}  where non-homogeneous Dirichlet conditions are imposed. We are then looking for the solution of a partial differential equation satisfying a Dirichlet and a Neumann boundary condition simultaneously on the free boundary. The existence and uniqueness of a solution have already been addressed and this paper is devoted first to the study of geometric and asymptotic properties of the solution and then to the numerical treatment of the problem using a shape optimization formulation. The major difficulty and originality of this paper lies in the treatment of the geometric constraints.

The level set method has become widely used in shape optimization where it allows a popular implementation of the steepest descent method. Once coupled with a ersatz material approximation [Allaire et al., J. Comput. Phys.194 (2004) 363–393], a single mesh is only used leading to very efficient and cheap numerical schemes in optimization of structures. However, it has some limitations and cannot be applied in every situation. This work aims at exploring such a limitation. We estimate the systematic error committed by using the ersatz material approximation and, on a model case, explain that they amplifies instabilities by a second order analysis of the objective function.

The paper deals with the genericity of domain-dependent spectral properties of the Laplacian-Dirichlet operator. In particular we prove that, generically, the squares of the eigenfunctions form a free family. We also show that the spectrum is generically non-resonant. The results are obtained by applying global perturbations of the domains and exploiting analytic perturbation properties.The work is motivated by two applications: an existence result for the problem of maximizing the rate of exponential decay of a damped membrane and an approximate controllability result for the bilinear Schrödinger equation.

We study the potential which minimizes the fundamental gap of theSchrödinger operator under the total mass constraint. We considerthe relaxed potential and prove a regularity result for the optimalone, we also give a description of it. A consequence of this resultis the existence of an optimal potential under L 1 constraints.

The aim of this article is to prove a symmetry result for several overdetermined boundary value problems. For the two first problems, our method combines the maximum principle with the monotonicity of the mean curvature. For the others, we use essentially the compatibility condition of the Neumann problem.