We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We study the notion of non-trivial elementary embeddings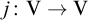 
under the assumption that V satisfies ZFC without Power Set but with the Collection Scheme. We show that no such embedding can exist under the additional assumption that it is cofinal and either 
is a set or that the scheme of Dependent Choices of arbitrary length holds. We then study failures of instances of Collection in symmetric submodels of class forcings.
