We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Consider the equation
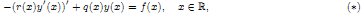
where ƒ ∈ Lp(ℝ), p ∈ (1, ∞) and
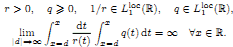
By a solution of (*), we mean any function y absolutely continuous together with (ry′) and satisfying (*) almost everywhere on ℝ. In addition, we assume that (*) is correctly solvable in the space Lp(ℝ), i.e.
(1) for any function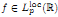 
, there exists a unique solution y ∈ Lp(ℝ) of (*);
(2) there exists an absolute constant c1(p) > 0 such that the solution y ∈ Lp(ℝ) of (*) satisfies the inequality
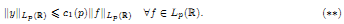
We study the following problem on the strengthening estimate (**). Let a non-negative function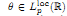 
be given. We have to find minimal additional restrictions for θ under which the following inequality holds:
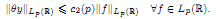
Here, y is a solution of (*) from the class Lp(ℝ), and c2 (p) is an absolute positive constant.
