We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let 
$R$ be an associative ring with unity. Then $R$ is said to be a right McCoy ring when the equation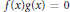 
$f\left( x \right)g\left( x \right)\,=\,0$ (over 
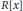$R\left[ x \right]$), where 
$0\,\ne \,f\left( x \right)$, 
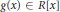$g\left( x \right)\,\in \,R\left[ x \right]$, implies that there exists a nonzero element 
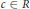$c\,\in \,R$ such that 
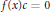$f\left( x \right)c\,=\,0$. In this paper, we characterize some basic ring extensions of right McCoy rings and we prove that if $R$ is a right McCoy ring, then
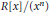$R\left[ x \right]/\left( {{x}^{n}} \right)$
is a right McCoy ring for any positive integer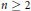 
$n\,\ge \,2$.
