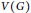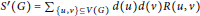Let $G$ be a connected graph with vertex set $V\left( G \right)$.The degree Kirchhoff index of $G$ is defined as ${{S}^{\prime }}\left( G \right)\,=\,\sum{_{\left\{ u,v \right\}\,\subseteq \,V\left( G \right)}d\left( u \right)d\left( v \right)R\left( u,\,v \right)}$, where 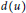$d\left( u \right)$ is the degree of vertex $u$, and 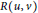$R\left( u,\,v \right)$ denotes the resistance distance between vertices $u$ and $v$. In this paper, we characterize the graphs having maximum and minimum degree Kirchhoff index among all $n$-vertex bicyclic graphs with exactly two cycles.

Given a connected regular graph $G$, let $l(G)$ be its line graph, $s(G)$ its subdivision graph, $r(G)$ the graph obtained from $G$ by adding a new vertex corresponding to each edge of $G$ and joining each new vertex to the end vertices of the corresponding edge and $q(G)$ the graph obtained from $G$ by inserting a new vertex into every edge of $G$ and new edges joining the pairs of new vertices which lie on adjacent edges of $G$. A formula for the normalised Laplacian characteristic polynomial of $l(G)$ (respectively $s(G),r(G)$ and $q(G)$) in terms of the normalised Laplacian characteristic polynomial of $G$ and the number of vertices and edges of $G$ is developed and used to give a sharp lower bound for the degree-Kirchhoff index and a formula for the number of spanning trees of $l(G)$ (respectively $s(G),r(G)$ and $q(G)$).