We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let 
$R$ be a commutative ring with identity, and let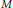 
$M$ be a unitary module over 
$R$. We call 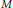$M$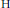
$\text{H}$-smaller (
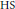$\text{HS}$ for short) if and only if 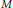$M$ is infinite and 
$\left| M/N \right|\,<\,\,\left| M \right|$ for every nonzero submodule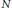 
$N$ of 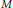$M$. After a brief introduction, we show that there exist nontrivial examples of HS modules of arbitrarily large cardinality over Noetherian and non-Noetherian domains. We then prove the following result: suppose 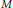$M$ is faithful over $R$, $R$ is a domain (we will show that we can restrict to this case without loss of generality), and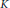 
$K$ is the quotient field of $R$. If 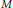$M$ is 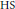$\text{HS}$ over 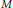$R$, then $R$ is 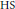$\text{HS}$ as a module over itself, 
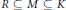$R\,\subseteq \,M\,\subseteq \,K$, and there exists a generating set 
$S$ for 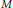$M$ over $R$ with 
$\left| S \right|\,<\,\left| R \right|$. We use this result to generalize a problem posed by Kaplansky and conclude the paper by answering an open question on Jónsson modules.
