We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Given two (real) normed (linear) spaces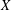 
$X$ and 
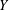$Y$, let 
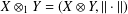$X\otimes _{1}Y=(X\otimes Y,\Vert \cdot \Vert )$, where 
$\Vert (x,y)\Vert =\Vert x\Vert +\Vert y\Vert$. It is known that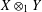 
$X\otimes _{1}Y$ is 
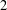$2$-UR if and only if both 
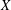$X$ and 
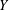$Y$ are UR (where we use UR as an abbreviation for uniformly rotund). We prove that if 
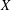$X$ is 
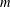$m$-dimensional and 
$Y$ is 
$k$-UR, then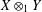 
$X\otimes _{1}Y$ is 
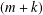$(m+k)$-UR. In the other direction, we observe that if 
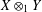$X\otimes _{1}Y$ is 
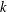$k$-UR, then both 
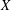$X$ and 
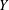$Y$ are 
$(k-1)$-UR. Given a monotone norm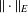 
$\Vert \cdot \Vert _{E}$ on 
$\mathbb{R}^{2}$, we let 
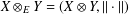$X\otimes _{E}Y=(X\otimes Y,\Vert \cdot \Vert )$ where 
$\Vert (x,y)\Vert =\Vert (\Vert x\Vert _{X},\Vert y\Vert _{Y})\Vert _{E}$. It is known that if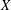 
$X$ is uniformly rotund in every direction, 
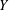$Y$ has the weak fixed point property for nonexpansive maps (WFPP) and 
$\Vert \cdot \Vert _{E}$ is strictly monotone, then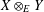 
$X\otimes _{E}Y$ has WFPP. Using the notion of 
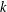$k$-uniform rotundity relative to every 
$k$-dimensional subspace we show that this result holds with a weaker condition on 
$X$.
