For a partially multiplicative quandle (PMQ) 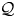${\mathcal {Q}}$ we consider the topological monoid 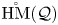$\mathring {\mathrm {HM}}({\mathcal {Q}})$ of Hurwitz spaces of configurations in the plane with local monodromies in 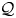${\mathcal {Q}}$. We compute the group completion of 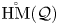$\mathring {\mathrm {HM}}({\mathcal {Q}})$: it is the product of the (discrete) enveloping group 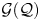${\mathcal {G}}({\mathcal {Q}})$ with a component of the double loop space of the relative Hurwitz space 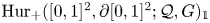$\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$; here 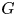$G$ is any group giving rise, together with 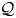${\mathcal {Q}}$, to a PMQ–group pair. Under the additional assumption that 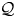${\mathcal {Q}}$ is finite and rationally Poincaré and that 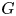$G$ is finite, we compute the rational cohomology ring of 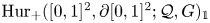$\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$.

Let $\pi$ be a discrete group, and let $G$ be a compact-connected Lie group. Then, there is a map $\Theta \colon \mathrm {Hom}(\pi,G)_0\to \mathrm {map}_*(B\pi,BG)_0$ between the null components of the spaces of homomorphisms and based maps, which sends a homomorphism to the induced map between classifying spaces. Atiyah and Bott studied this map for $\pi$ a surface group, and showed that it is surjective in rational cohomology. In this paper, we prove that the map $\Theta$ is surjective in rational cohomology for $\pi =\mathbb {Z}^m$ and the classical group $G$ except for $SO(2n)$, and that it is not surjective for $\pi =\mathbb {Z}^m$ with $m\ge 3$ and $G=SO(2n)$ with $n\ge 4$. As an application, we consider the surjectivity of the map $\Theta$ in rational cohomology for $\pi$ a finitely generated nilpotent group. We also consider the dimension of the cokernel of the map $\Theta$ in rational homotopy groups for $\pi =\mathbb {Z}^m$ and the classical groups $G$ except for $SO(2n)$.

We compute the rational cohomology of the moduli space of non-singular complex plane quartic curves with two marked points. This allows us to calculate the rational cohomology of the moduli space of non-singular complex projective curves of genus three with two marked points.

We compute the mixed Hodge structure on the rational cohomology of the moduli space of smooth genus 4 curves. Specifically, we prove that its Poincaré–Serre polynomial is 1 + t2u2 + t4u4 + t5u6. We show this by producing a stratification of the space, such that all strata are geometric quotients of complements of discriminants.