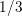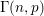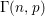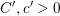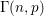Let 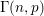 ${\rm\Gamma}(n,p)$ denote the binomial model of a random triangular group. We show that there exist constants
${\rm\Gamma}(n,p)$ denote the binomial model of a random triangular group. We show that there exist constants  $c,C>0$ such that if
$c,C>0$ such that if  $p\leqslant c/n^{2}$, then asymptotically almost surely (a.a.s.)
$p\leqslant c/n^{2}$, then asymptotically almost surely (a.a.s.)  ${\rm\Gamma}(n,p)$ is free, and if
${\rm\Gamma}(n,p)$ is free, and if  $p\geqslant C\log n/n^{2}$, then a.a.s.
$p\geqslant C\log n/n^{2}$, then a.a.s. 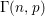 ${\rm\Gamma}(n,p)$ has Kazhdan’s property (T). Furthermore, we show that there exist constants
${\rm\Gamma}(n,p)$ has Kazhdan’s property (T). Furthermore, we show that there exist constants 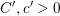 $C^{\prime },c^{\prime }>0$ such that if
$C^{\prime },c^{\prime }>0$ such that if  $C^{\prime }/n^{2}\leqslant p\leqslant c^{\prime }\log n/n^{2}$, then a.a.s.
$C^{\prime }/n^{2}\leqslant p\leqslant c^{\prime }\log n/n^{2}$, then a.a.s. 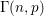 ${\rm\Gamma}(n,p)$ is neither free nor has Kazhdan’s property (T).
${\rm\Gamma}(n,p)$ is neither free nor has Kazhdan’s property (T).
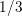 $1/3$
$1/3$