We prove that qu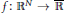asiconvex functions always admit descent trajectories bypassing all nonminimizing critical points.

We prove that if $f\,:\,{{\mathbb{R}}^{N}}\,\to \,\overline{\mathbb{R}}$ is quasiconvex and $U\,\subset \,{{\mathbb{R}}^{N}}$ is open in the density topology, then $\underset{U}{\mathop{\sup }}\,f=\text{ess}\,\underset{U}{\mathop{\sup }}\,f$, while 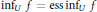${{\inf }_{U}}\,f\,=\,\text{ess}\,{{\inf }_{U}}\,f$ if and only if the equality holds when $U\,\subset \,{{\mathbb{R}}^{N}}$. The first (second) property is typical of 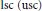$\text{lsc}\,\text{(usc)}$ functions, and, even when 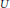$U$ is an ordinary open subset, there seems to be no record that they both hold for all quasiconvex functions.

This property ensures that the pointwise extrema of 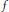$f$ on any nonempty density open subset can be arbitrarily closely approximated by values of 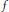$f$ achieved on “large” subsets, which may be of relevance in a variety of situations. To support this claim, we use it to characterize the common points of continuity, or approximate continuity, of two quasiconvex functions that coincide away from a set of measure zero.

In this paper we propose an extension of the proximal point method to solve minimization problems with quasiconvex objective functions on Hadamard manifolds. To reach this goal, we initially extend the concepts of regular and generalized subgradient from Euclidean spaces to Hadamard manifolds and prove that, in the convex case, these concepts coincide with the classical one. For the minimization problem, assuming that the function is bounded from below, in the quasiconvex and lower semicontinuous case, we prove the convergence of the iterations given by the method. Furthermore, under the assumptions that the sequence of proximal parameters is bounded and the function is continuous, we obtain the convergence to a generalized critical point. In particular, our work extends the applications of the proximal point methods for solving constrained minimization problems with nonconvex objective functions in Euclidean spaces when the objective function is convex or quasiconvex on the manifold.

Motivated by the study of multidimensional control problems of Dieudonné-Rashevsky type, we raise the question how to understand to notion of quasiconvexity for a continuous function f with a convex body K $\subset \mathbb{R}^{nm}$ instead of the whole space $\mathbb{R}^{nm}$ as the range of definition. In the present paper, we trace the consequences of an infinite extension of f outside K, and thus study quasiconvex functions which are allowed to take the value +∞. As an appropriate envelope, we introduce and investigate the lower semicontinuous quasiconvex envelope $f^{(qc)} (v) = {\rm sup} \{ \,g(v)\, \vert \,g : \mathbb{R}^{nm} \rightarrow \mathbb{R} \cup \{ + \infty \}$ quasiconvex and lower semicontinuous, $g(v) \leq f(v) \,\,\,\,\forall v \in \mathbb{R}^{nm}\,\}.$ Our main result is a representation theorem for $f^{({\it qc})}$ which generalizes Dacorogna's well-known theorem on the representation of the quasiconvex envelope of a finite function. The paper will be completed by the calculation of $f^{({\it qc})}$ in two examples.