We introduce a relaxed version of the metric definition of quasiconformality that is natural also for mappings of low regularity, including $W_{\mathrm{loc}}^{1,1}({\mathbb R}^n;{\mathbb R}^n)$-mappings. Then we show on the plane that this relaxed definition can be used to prove Sobolev regularity, and that these ‘finely quasiconformal’ mappings are in fact quasiconformal.

Zhou et al. [‘On weakly non-decreasable quasiconformal mappings’, J. Math. Anal. Appl.386 (2012), 842–847] proved that, in a Teichmüller equivalence class, there exists an extremal quasiconformal mapping with a weakly nondecreasable dilatation. They asked whether a weakly nondecreasable dilatation is a nondecreasable dilatation. The aim of this paper is to give a negative answer to their problem. We also construct a Teichmüller class such that it contains an infinite number of weakly nondecreasable extremal representatives, only one of which is nondecreasable.

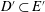Suppose that $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}E$ and $E'$ denote real Banach spaces with dimension at least 2 and that $D\subset E$ and $D'\subset E'$ are domains. Let 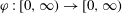$\varphi :[0,\infty )\to [0,\infty )$ be a homeomorphism with 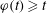$\varphi (t)\geq t$. We say that a homeomorphism $f: D\to D'$ is $\varphi $-FQC if for every subdomain $D_1 \subset D$, we have $\varphi ^{-1} (k_D(x,y))\leq k_{D'} (f(x),f(y))\leq \varphi (k_D(x,y))$ holds for all $x,y\in D_1$. In this paper, we establish, in terms of the 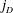$j_D$ metric, a necessary and sufficient condition for a homeomorphism $f: E \to E'$ to be FQC. Moreover, we give, in terms of the $j_D$ metric, a sufficient condition for a homeomorphism $f: D\to D'$ to be FQC. On the other hand, we show that this condition is not necessary.