We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
$S_{n}^{+}$
Motivated by a question of A. Skalski and P. M. Sołtan (2016) about inner faithfulness of S. Curran’s map of extending a quantum increasing sequence to a quantum permutation, we revisit the results and techniques of T. Banica and J. Bichon (2009) and study some group-theoretic properties of the quantum permutation group on points. This enables us not only to answer the aforementioned question in the positive for the case where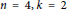 
$n\,=\,4,\,k\,=\,2$, but also to classify the automorphisms of 
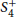$S_{4}^{+}$, describe all the embeddings 
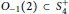${{O}_{-1}}(2)\,\subset \,S_{4}^{+}$ and show that all the copies of 
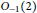${{O}_{-1}}(2)$ inside 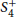$S_{4}^{+}$are conjugate. We then use these results to show that the converse to the criterion we applied to answer the aforementioned question is not valid.
