We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We find a lower bound on the number of imaginary quadratic extensions of the function field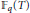 
${{\mathbb{F}}_{q}}\left( T \right)$ whose class groups have an element of a fixed order.
More precisely, let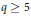 
$q\,\ge \,5$ be a power of an odd prime and let 
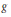$g$ be a fixed positive integer 
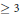$\ge \,3$. There are 
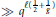$\gg \,{{q}^{\ell \left( \frac{1}{2}+\frac{1}{g} \right)}}$ polynomials 
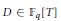$D\,\in \,{{\mathbb{F}}_{q}}\left[ T \right]$ with 
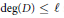$\deg \left( D \right)\,\le \,\ell $ such that the class groups of the quadratic extensions 
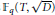${{\mathbb{F}}_{q}}\left( T,\,\sqrt{D} \right)$ have an element of order 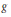$g$.
