Search

We show, under some natural restrictions, that some semigroup orbits of polynomials cannot contain too many elements of small multiplicative order modulo a large prime 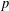$p$, extending previous work of Shparlinski [‘Multiplicative orders in orbits of polynomials over finite fields’, Glasg. Math. J.60(2) (2018), 487–493].

Let f be a complex polynomial mapping. We relate the behaviour of f ’at infinity‘ to the characteristic cycle associated to the projective closures of fibres of f. We obtain a condition on the characteristic cycle which is equivalent to a condition on the asymptotic behaviour of some of the minors of the Jacobian matrix of f. This condition generalizes the condition in the hypersurface case known as Malgrange‘s condition. The relation between this condition and the behavior of the characteristic cycle is a partial generalization of Parusinski‘s result in the hypersurface case. We show that the new condition implies the C$^∞$-triviality of f.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

ON SEMIGROUP ORBITS OF POLYNOMIALS AND MULTIPLICATIVE ORDERS

Fibers of Polynomial Mappings at Infinity and a Generalized Malgrange Condition

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

ON SEMIGROUP ORBITS OF POLYNOMIALS AND MULTIPLICATIVE ORDERS

Fibers of Polynomial Mappings at Infinity and a Generalized Malgrange Condition