We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let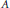 
$A$ be a ring with local units, 
$E$ a set of local units for 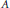$A$,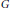 
$G$ an abelian group, and 
$\alpha$ a partial action of 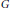$G$ by ideals of 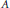$A$ that contain local units. We show that 
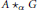$\text{A}\,{{\star }_{\alpha }}\,G$ is simple if and only if 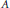$A$ is 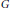$G$-simple and the center of the corner 
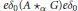$e{{\delta }_{0}}\left( \text{A}\,{{\star }_{\alpha }}\,G \right)e{{\delta }_{0}}$ is a field for all 
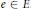$e\,\in \,E$. We apply the result to characterize simplicity of partial skew group rings in two cases, namely for partial skew group rings arising from partial actions by clopen subsets of a compact set and partial actions on the set level.
