We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
On post-critically finite self-similar sets, whose walk dimensions of diffusions are in general larger than 2, we find a sharp region where two classes of Besov spaces, the heat Besov spaces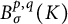 
$B^{p,q}_\sigma (K)$ and the Lipschitz–Besov spaces 
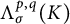$\Lambda ^{p,q}_\sigma (K)$, are identical. In particular, we provide concrete examples that 
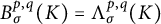$B^{p,q}_\sigma (K)=\Lambda ^{p,q}_\sigma (K)$ with 
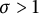$\sigma>1$. Our method is purely analytical, and does not involve heat kernel estimate.
