Historians have written copiously about the shift to ‘germ theories’ of disease around the turn of the twentieth century, but in these accounts an entire continent has been left out: Antarctica. This article begins to rebalance our historiography by bringing cold climates back into the story of environmental medicine and germ theory. It suggests three periods of Antarctic (human) microbial research – heroic sampling, systematic studies, and viral space analogue – and examines underlying ideas about ‘purity’ and infection, the realities of fieldwork, and the use of models in biomedicine. It reveals Antarctica not as an isolated space but as a deeply complex, international, well-networked node in global science ranging from the first international consensus on pandemic-naming through to space flight.

Human capacity to explore and shape outer space will increase substantially over the next 50 years. Yet, International Relations (IR) theory still treats outer space as an isolated, unique, or inconsequential realm of political life. This paper moves IR beyond its ‘terrestrial trap’ by theorising planetary politics as inherently embedded in relations with environments and actors that are located beyond Earth. To face the momentous and often alarming political developments taking place in outer space, from space militarisation to space colonisation, we challenge two of IR’s terrestrial biases. First, we confront the assumption that developments in international relations take place only or primarily on Earth. We show how the historically constituted ideologies and political economies of colonisation and domination are extended to – but also transformed within – outer space exploration and settlement. Second, we challenge the notion that developments in outer space form a logical extension of politics as it has emerged on the habitable surface of our planet. We move beyond zones of human habitation and explore how the material conditions of space intersect with situated histories of political governance and control. By analysing politics beyond Earth, we retool IR theory to confront an extraterrestrial political future.

We construct an unfolding path in Outer space which does not converge in the boundary, and instead it accumulates on the entire 1-simplex of projectivized length measures on a nongeometric arational ${\mathbb R}$-tree T. We also show that T admits exactly two dual ergodic projective currents. This is the first nongeometric example of an arational tree that is neither uniquely ergodic nor uniquely ergometric.

The 1967 Outer Space Treaty reserved outer space for ‘peaceful purposes’, yet recent decades have witnessed growing competition and calls for new multilateral rules including a proposed ban on the deployment of weapons in space. These diplomatic initiatives have stalled in the face of concerted opposition from the United States. To explain this outcome, we characterise US diplomacy as a form of ‘antipreneurship’, a type of strategic norm-focused competition designed to preserve the prevailing normative status quo in the face of entrepreneurial efforts. We substantially refine and extend existing accounts of antipreneurship by theorising three dominant forms of antipreneurial agency – rhetorical, procedural, and behavioural – and describing the mechanisms and scope conditions though which they operate. We then trace the development of US resistance to proposed restraints on space weapons from 2000–present. Drawing on hundreds of official documents, we show how successive US administrations have employed a range of interlayered diplomatic strategies and tactics to preserve the permissive international legal framework governing outer space and protect US national security priorities. Our study illustrates the specific techniques and impacts of resistance in a domain of growing strategic importance, with implications for further refining understandings of norm competition in other issue areas.

The quantity of man-made space objects, ranging from abandoned launch vehicle stages to fragmentation debris, is remarkable. At the time, the drafters of the Outer Space Treaty did not (and perhaps could not) anticipate how great the problem of debris in outer space would one day become. As a result, they only drafted general provisions for the protection of the space environment which are generally deemed insufficient. This article aims to demonstrate that both general rules of international law and the UNCOPUOS Debris Mitigation Guidelines come to the rescue in addressing the space debris issue as they complement and complete the general obligations contained in the Outer Space Treaty. Particular attention is paid to anti-satellite weapon tests, which have catastrophic consequences in terms of creating debris but nonetheless continue to be carried out. Finally, it ascertains whether an obligation on states to actively remove their space debris exists.

In this paper we consider two piecewise Riemannian metrics defined on the Culler–Vogtmann outer space which we call the entropy metric and the pressure metric. As a result of work of McMullen, these metrics can be seen as analogs of the Weil–Petersson metric on the Teichmüller space of a closed surface. We show that while the geometric analysis of these metrics is similar to that of the Weil–Petersson metric, from the point of view of geometric group theory, these metrics behave very differently than the Weil–Petersson metric. Specifically, we show that when the rank r is at least 4, the action of $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$ on the completion of the Culler–Vogtmann outer space using the entropy metric has a fixed point. A similar statement also holds for the pressure metric.

How does a ‘space culture’ emerge and evolve, and how can archaeologists study such a phenomenon? The International Space Station Archaeological Project seeks to analyse the social and cultural context of an assemblage relating to the human presence in space. Drawing on concepts from contemporary archaeology, the project pursues a unique perspective beyond sociological or ethnographical approaches. Semiotic analysis of material culture and proxemic analysis of embodied space can be achieved using NASA's archives of documentation, images, video and audio media. Here, the authors set out a method for the study of this evidence. Understanding how individuals and groups use material culture in space stations, from discrete objects to contextual relationships, promises to reveal intersections of identity, nationality and community.

Security concerns during the early Cold War prompted United States strategists to solicit worldwide assistance in studying Earth’s physical environment. Comprehensive geophysical knowledge required cooperation between researchers on every part of the planet, leading practitioners to tout transnational earth science – despite direct military applications in an age of submarines and ballistic missiles – as a non-political form of peaceful universalism. This article examines the 1957–58 International Geophysical Year as a powerful fulcrum in the transfer of ideas about Earth’s global environment from Western security establishments to conservationists worldwide. For eighteen months, tens of thousands of researchers across every continent pooled resources for data collection to create a scientific benchmark for future comparisons. Illuminating Earth as dynamic and interconnected, participants robustly conceptualized humanity’s emergence as a geophysical force, capable of ‘artificially’ modifying the natural world. Studies of anthropogenic geophysics, including satellites, nuclear fallout, and climate change, conditioned the global rise of environmentalism.

There are at least four ways in which Antarctic colonialism was white: it was paradigmatically performed by white men; it consisted in the taking of vast, white expanses of land; it was carried out with a carte blanche (literally, “blank card”) attitude; and it was presented to the world as a white, innocent adventure. While the first, racial whiteness has been amply problematised, I suggest that the last three illuminate yet other moral wrongs of the Antarctic colonial project. Moreover, they might be constitutive of a larger class of “white” colonialisms beyond the White Continent.

This study assesses China's approach to the global commons, those areas of the globe over which no state exercises sovereignty and that are accessible to all. Examining Chinese behaviour, official statements and expert positions towards the extant high seas and outer space regimes, this research concludes that China approaches the principle of international access to the two domains situationally, reflecting its assessment of how these regimes affect its national interests. The finding cautions against blanket characterizations of China's strategic orientation towards the global commons.

Outer space is becoming a more accessible and less expensive domain in which to operate. Consequently, growing numbers of state and non-state actors (NSAs) are operating in, to, and through space. At the same time, instances of space-based and ground-based interference with space systems are also increasing, disrupting crucial space-supported services and applications relied on by millions, with great financial and operational costs. The increased participation of NSAs in space activities raises particular concerns, especially the threat of intentional interference with space systems by nefarious actors like terrorist organizations. It also requires consideration of whether states bear responsibility and/or liability for the acts of NSAs with a nexus to those states. At first glance, it is tempting to conclude that one or more normative legal regimes would apply. The potential regimes include international space law, international telecommunications law, and the law of state responsibility. On further examination, however, when it comes to interference, there appears to be no effective legal mechanism to hold states accountable for NSA interference with space systems, which can be exploited by NSAs and challenge efforts by states to enforce “good” behaviour.

Culler and Vogtmann defined a simplicial space 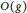$O\left( g \right)$, called outer space, to study the outer automorphism group of the free group 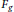${{F}_{g}}$. Using representation theoretic methods, we give an embedding of 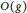$O\left( g \right)$ into the analytification of $x\left( {{F}_{g}}\,,\,S{{L}_{2}}\left( \mathbb{C} \right) \right)$, the 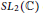$S{{L}_{2}}\left( \mathbb{C} \right)$ character variety of 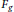${{F}_{g}}$, reproving a result of Morgan and Shalen. Then we show that every point $v$ contained in a maximal cell of 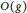$O\left( g \right)$ defines a flat degeneration of $x\left( {{F}_{g}}\,,\,S{{L}_{2}}\left( \mathbb{C} \right) \right)$ to a toric variety $X\left( {{P}_{\Gamma }} \right)$. We relate $x\left( {{F}_{g}}\,,\,S{{L}_{2}}\left( \mathbb{C} \right) \right)$ and 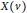$X\left( v \right)$ topologically by showing that there is a surjective, continuous, proper map 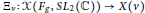${{\Xi }_{v}}\,:\,x\left( {{F}_{g}}\,,\,S{{L}_{2}}\,\left( \mathbb{C} \right) \right)\,\to \,X\left( v \right)$. We then show that this map is a symplectomorphism on a dense open subset of $x\left( {{F}_{g}}\,,\,S{{L}_{2}}\left( \mathbb{C} \right) \right)$ with respect to natural symplectic structures on $x\left( {{F}_{g}}\,,\,S{{L}_{2}}\left( \mathbb{C} \right) \right)$ and 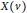$X\left( v \right)$. In this way, we construct an integrable Hamiltonian system in $x\left( {{F}_{g}}\,,\,S{{L}_{2}}\left( \mathbb{C} \right) \right)$ for each point in a maximal cell of 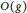$O\left( g \right)$, and we show that each $v$ defines a topological decomposition of $x\left( {{F}_{g}}\,,\,S{{L}_{2}}\left( \mathbb{C} \right) \right)$ derived from the decomposition of $X\left( {{P}_{\Gamma }} \right)$ by its torus orbits. Finally, we show that the valuations coming from the closure of a maximal cell in 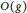$O\left( g \right)$ all arise as divisorial valuations built from an associated projective compactification of $x\left( {{F}_{g}}\,,\,S{{L}_{2}}\left( \mathbb{C} \right) \right)$.