We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper, the 
$L^p(\mathbb{R})\times L^q(\mathbb{R})\rightarrow L^r(\mathbb{R})$ boundedness of the bilinear oscillatory integral along parabolais set up, where β > 1 or β < 0, 
\begin{equation*}T_\beta(f, g)(x)=p.v.\int_{{\mathbb R}} f(x-t)g(x-t^{2})\,{\rm e}^{i |t|^{\beta}}\,\frac{{\rm d}t}{t}\end{equation*}
$\frac{1}{p}+\frac{1}{q}=\frac{1}{r}$ and 
$\frac{1}{2}\lt r\lt\infty$, p > 1 and q > 1. The result for the case β < 0 extends the 
$L^\infty\times L^2\to L^2$ boundedness obtained by Fan and Li (D. Fan and X. Li, A bilinear oscillatory integral along parabolas, Positivity 13(2) (2009), 339–366) by confirming an open question raised in it.
In this paper, the bounded properties of oscillatory hyper-Hilbert transformalong certain plane curves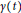 
$\gamma \left( t \right)$,
$${{T}_{\alpha ,\beta }}f\left( x,\,y \right)\,=\,\int_{0}^{1}{f\left( x\,-\,t,\,y\,-\,\gamma \left( t \right) \right){{e}^{i{{t}^{-\beta }}}}\frac{\text{d}t}{{{t}^{1}}+\alpha }}$$
are studied. For general curves, these operators are bounded in 
${{L}^{2}}\left( {{\mathbb{R}}^{2}} \right)$ if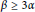 
$\beta \,\ge \,3\alpha $. Their boundedness in ${{L}^{p}}\left( {{\mathbb{R}}^{2}} \right)$ is also obtained, whenever 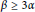$\beta \,\ge \,3\alpha $ and 
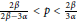$\frac{2\beta }{2\beta -3\alpha }\,<\,p\,<\,\frac{2\beta }{3\alpha }$.
${ \mathbb{R} }^{3} $
In this paper we obtain some sharp 
${L}^{p} - {L}^{q} $ estimates and the restricted weak-type endpoint estimates for the multiplier operator of negative order associated with conic surfaces in 
${ \mathbb{R} }^{3} $ which have finite type degeneracy.
