Given a positive integer  $n$, a finite field
$n$, a finite field 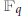 ${{\mathbb{F}}_{q}}$ of
${{\mathbb{F}}_{q}}$ of  $q$ elements (
$q$ elements ( $q$ odd), and a non-degenerate symmetric bilinear form
$q$ odd), and a non-degenerate symmetric bilinear form  $B$ on
$B$ on 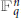 $\mathbb{F}_{q}^{n}$, we determine the largest possible cardinality of pairwise
$\mathbb{F}_{q}^{n}$, we determine the largest possible cardinality of pairwise  $B$-orthogonal subsets
$B$-orthogonal subsets 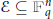 $\varepsilon \,\subseteq \,\mathbb{F}_{q}^{n}$, that is, for any two vectors
$\varepsilon \,\subseteq \,\mathbb{F}_{q}^{n}$, that is, for any two vectors  $x,\,y\,\in \,\varepsilon $, one has
$x,\,y\,\in \,\varepsilon $, one has 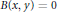 $B(x,\,y)\,=\,0$.
$B(x,\,y)\,=\,0$.