We provide a short proof that if κ is a regular cardinal with κ < c, then
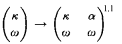
for any ordinal α < min{ , κ}. In particular,
, κ}. In particular,
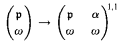
for any ordinal α <  . This generalizes an unpublished result of E. Szemerédi that Martin's axiom implies that
. This generalizes an unpublished result of E. Szemerédi that Martin's axiom implies that
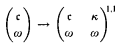
for any cardinal κ with κ < c.