We prove that if two normed-algebra-valued cosine families indexed by a single Abelian group, of which one is bounded and comprised solely of scalar elements of the underlying algebra, differ in norm by less than 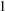 $1$ uniformly in the parametrising index, then these families coincide.
$1$ uniformly in the parametrising index, then these families coincide.