We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We consider the parabolic one-dimensional Allen–Cahn equation
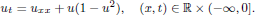
The steady state 
connects, as a ‘transition layer’, the stable phases –1 and +1. We construct a solution u with any given number k of transition layers between –1 and +1. Mainly they consist of k time-travelling copies of w, with each interface diverging as t → –∞. More precisely, we find
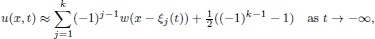
where the functions ξj (t) satisfy a first-order Toda-type system. They are given by
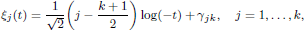
for certain explicit constants γjk.
