The study carried out in this paper about some new examples of Banach spaces, consisting of certain valued fields extensions, is a typical non-archimedean feature. We determine whether these extensions are of countable type, have  $t$-orthogonal bases, or are reflexive. As an application we construct, for a class of base fields, a norm
$t$-orthogonal bases, or are reflexive. As an application we construct, for a class of base fields, a norm 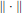 $\left\| \,.\, \right\|$ on
$\left\| \,.\, \right\|$ on  ${{c}_{0}}$, equivalent to the canonical supremum norm, without non-zero vectors that are
${{c}_{0}}$, equivalent to the canonical supremum norm, without non-zero vectors that are 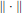 $\left\| \,.\, \right\|$-orthogonal and such that there is a multiplication on
$\left\| \,.\, \right\|$-orthogonal and such that there is a multiplication on  ${{c}_{0}}$ making
${{c}_{0}}$ making 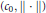 $\left( {{c}_{0}},\,\left\| \,.\, \right\| \right)$ into a valued field.
$\left( {{c}_{0}},\,\left\| \,.\, \right\| \right)$ into a valued field.