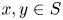A set of complex numbers $S$ is called invariant if it is closed under addition and multiplication, namely, for any $x, y \in S$ we have $x+y \in S$ 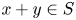and $xy \in S$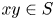. For each $s \in {\mathbb {C}}$ the smallest invariant set ${\mathbb {N}}[s]$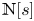 containing $s$ 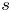consists of all possible sums $\sum _{i \in I} a_i s^i$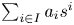, where $I$ 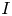runs over all finite nonempty subsets of the set of positive integers ${\mathbb {N}}$ 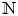and $a_i \in {\mathbb {N}}$ for each $i \in I$. 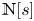In this paper, we prove that for $s \in {\mathbb {C}}$ the set ${\mathbb {N}}[s]$ is everywhere dense in ${\mathbb {C}}$ 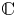if and only if $s \notin {\mathbb {R}}$ 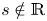and $s$ 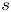is not a quadratic algebraic integer. More precisely, we show that if $s \in {\mathbb {C}} \setminus {\mathbb {R}}$ 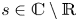is a transcendental number, then there is a positive integer $n$ such that the sumset ${\mathbb {N}} t^n+{\mathbb {N}} t^{2n} +{\mathbb {N}} t^{3n}$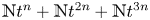 is everywhere dense in ${\mathbb {C}}$ for either $t=s$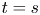 or $t=s+s^2$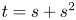. Similarly, if $s \in {\mathbb {C}} \setminus {\mathbb {R}}$ 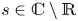is an algebraic number of degree $d \ne 2, 4$, then there are positive integers $n, m$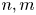 such that the sumset ${\mathbb {N}} t^n+{\mathbb {N}} t^{2n} +{\mathbb {N}} t^{3n}$ 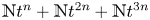is everywhere dense in ${\mathbb {C}}$ 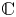for $t=ms+s^2$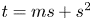. For quadratic and some special quartic algebraic numbers $s$ 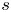it is shown that a similar sumset of three sets cannot be dense. In each of these two cases the density of ${\mathbb {N}}[s]$ 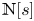in ${\mathbb {C}}$ 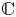is established by a different method: for those special quartic numbers, it is possible to take a sumset of four sets.