We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let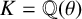 
$K={\mathbb {Q}}(\theta )$ be an algebraic number field with 
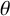$\theta $ satisfying a monic irreducible polynomial 
$f(x)$ of degree n over 
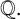${\mathbb {Q}}.$ The polynomial 
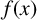$f(x)$ is said to be monogenic if 
$\{1,\theta ,\ldots ,\theta ^{n-1}\}$ is an integral basis of K. Deciding whether or not a monic irreducible polynomial is monogenic is an important problem in algebraic number theory. In an attempt to answer this problem for a certain family of polynomials, Jones [‘A brief note on some infinite families of monogenic polynomials’, Bull. Aust. Math. Soc. 100 (2019), 239–244] conjectured that if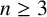 
$n\ge 3$, 
$1\le m\le n-1$,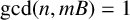 
$\gcd (n,mB)=1$ and A is a prime number, then the polynomial 
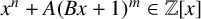$x^n+A (Bx+1)^m\in {\mathbb {Z}}[x]$ is monogenic if and only if 
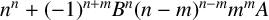$n^n+(-1)^{n+m}B^n(n-m)^{n-m}m^mA$ is square-free. We prove that this conjecture is true.
