Suppose that 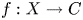$f:X\to C$ is a general Jacobian elliptic surface over 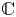${\mathbb {C}}$ of irregularity 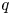$q$ and positive geometric genus 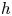$h$. Assume that 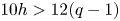$10 h>12(q-1)$, that 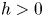$h>0$ and let 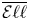$\overline {\mathcal {E}\ell \ell }$ denote the stack of generalized elliptic curves. 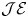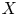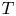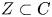(1) The moduli stack $\mathcal {JE}$ of such surfaces is smooth at the point $X$ and its tangent space $T$ there is naturally a direct sum of lines $(v_a)_{a\in Z}$, where $Z\subset C$ is the ramification locus of the classifying morphism 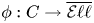$\phi :C\to \overline {\mathcal {E}\ell \ell }$ that corresponds to 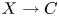$X\to C$. (2) For each 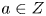$a\in Z$ the map 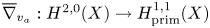$\overline {\nabla }_{v_a}:H^{2,0}(X)\to H^{1,1}_{\rm prim}(X)$ defined by the derivative 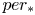$per_*$ of the period map $per$ is of rank one. Its image is a line 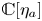${\mathbb {C}}[\eta _a]$ and its kernel is 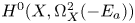$H^0(X,\Omega ^2_X(-E_a))$, where 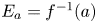$E_a=f^{-1}(a)$. (3) The classes 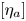$[\eta _a]$ form an orthogonal basis of 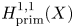$H^{1,1}_{\rm prim}(X)$ and 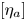$[\eta _a]$ is represented by a meromorphic $2$-form 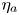$\eta _a$ in 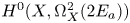$H^0(X,\Omega ^2_X(2E_a))$ of the second kind. (4) We prove a local Schottky theorem; that is, we give a description of 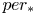$per_*$ in terms of a certain additional structure on the vector bundles that are involved. Assume further that 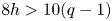$8h>10(q-1)$ and that 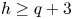$h\ge q+3$. (5) Given the period point 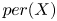$per(X)$ of 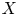$X$ that classifies the Hodge structure on the primitive cohomology 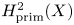$H^2_{\rm prim}(X)$ and the image of 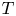$T$ under 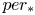$per_*$ we recover 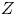$Z$ as a subset of 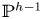${\mathbb {P}}^{h-1}$ and then, by quadratic interpolation, the curve 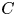$C$. (6) We prove a generic Torelli theorem for these surfaces. Everything relies on the construction, via certain kinds of Schiffer variations of curves, of certain variations of 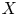$X$ for which 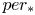$per_*$ can be calculated. (In an earlier version of this paper we used variations constructed by Fay. However, Schiffer variations are slightly more powerful.)

We show that the K-moduli spaces of log Fano pairs $\left(\mathbb {P}^1\times \mathbb {P}^1, cC\right)$ , where C is a $(4,4)$ curve and their wall crossings coincide with the VGIT quotients of $(2,4)$ , complete intersection curves in $\mathbb {P}^3$ . This, together with recent results by Laza and O’Grady, implies that these K-moduli spaces form a natural interpolation between the GIT moduli space of $(4,4)$ curves on $\mathbb {P}^1\times \mathbb {P}^1$ and the Baily–Borel compactification of moduli of quartic hyperelliptic K3 surfaces.

We study bundles on projective spaces that have vanishing lower cohomologies using their short minimal free resolutions. We partition the moduli $\mathcal{M}$ according to the Hilbert function H and classify all possible Hilbert functions H of such bundles. For each H, we describe a stratification of $\mathcal{M}_H$ by quotients of rational varieties. We show that the closed strata form a graded lattice given by the Betti numbers.

For complex connected, reductive, affine, algebraic groups G, we give a Lie-theoretic characterization of the semistability of principal G-co-Higgs bundles on the complex projective line ℙ1 in terms of the simple roots of a Borel subgroup of G. We describe a stratification of the moduli space in terms of the Harder–Narasimhan type of the underlying bundle.

By work of Looijenga and others, one understands the relationship between Geometric Invariant Theory (GIT) and Baily–Borel compactifications for the moduli spaces of degree-$2$ $K3$ surfaces, cubic fourfolds, and a few other related examples. The similar-looking cases of degree-$4$ $K3$ surfaces and double Eisenbud–Popescu–Walter (EPW) sextics turn out to be much more complicated for arithmetic reasons. In this paper, we refine work of Looijenga in order to handle these cases. Specifically, in analogy with the so-called Hassett–Keel program for the moduli space of curves, we study the variation of log canonical models for locally symmetric varieties of Type IV associated to $D$-lattices. In particular, for the $19$-dimensional case, we conjecturally obtain a continuous one-parameter interpolation between the GIT and Baily–Borel compactifications for the moduli of degree-$4$ $K3$ surfaces. The analogous $18$-dimensional case, which corresponds to hyperelliptic degree-$4$ $K3$ surfaces, can be verified by means of Variation of Geometric Invariant Theory (VGIT) quotients.

We study the dynamics of a singular holomorphic vector field at $(\mathbb{C}^{2},0)$. Using the associated flow and its pullback to the blow-up manifold, we provide invariants relating the vector field, a non-invariant analytic branch of curve, and the deformation of this branch by the flow. This leads us to study the conjugacy classes of singular branches under the action of holomorphic flows. In particular, we show that there exists an analytic class that is not complete, meaning that there are two elements of the class that are not analytically conjugated by a local biholomorphism embedded in a one-parameter flow. Our techniques are new and offer an approach dual to the one used classically to study singularities of holomorphic vector fields.

In this paper we prove that a smooth family of canonically polarized manifolds parametrized by a special (in the sense of Campana) quasi-projective variety is isotrivial.

We construct one-dimensional families of Abelian surfaces with quaternionic multiplication, which also have an automorphism of order three or four. Using Barth's description of the moduli space of (2,4)-polarized Abelian surfaces, we find the Shimura curve parametrizing these Abelian surfaces in a specific case. We explicitly relate these surfaces to the Jacobians of genus two curves studied by Hashimoto and Murabayashi. We also describe a (Humbert) surface in Barth's moduli space that parametrizes Abelian surfaces with real multiplication by $\mathbf{Z}\left[ \sqrt{2} \right]$ .

We prove a global Torelli theorem for pairs $(Y,D)$ where $Y$ is a smooth projective rational surface and $D\in |-K_{Y}|$ is a cycle of rational curves, as conjectured by Friedman in 1984. In addition, we construct natural universal families for such pairs.

We show that there is no stable Siegel modular form that vanishes on every moduli space of curves.

We study the stable pairs theory of local curves in 3-folds with descendent insertions. The rationality of the partition function of descendent invariants is established for the full local curve geometry (equivariant with respect to the scaling 2-torus), including relative conditions and odd-degree insertions for higher-genus curves. The capped 1-leg descendent vertex (equivariant with respect to the 3-torus) is also proven to be rational. The results are obtained by combining geometric constraints with a detailed analysis of the poles of the descendent vertex.

We study the moduli spaces of polarised irreducible symplectic manifolds. By a comparison with locally symmetric varieties of orthogonal type of dimension 20, we show that the moduli space of polarised deformation K3[2] manifolds with polarisation of degree 2d and split type is of general type if d≥12.

We classify del Pezzo surfaces with quotient singularities and Picard rank one which admit a ℚ-Gorenstein smoothing. These surfaces arise as singular fibres of del Pezzo fibrations in the 3-fold minimal model program and also in moduli problems.

We study, from the point of view of abelian and Kummer surfaces and their moduli, the special quintic threefold known as Nieto's quintic. It is, in some ways, analogous to the Segre cubic and the Burkhardt quartic and can be interpreted as a moduli space of certain Kummer surfaces. It contains 30 planes and has 10 singular points: we describe how some of these arise from bielliptic and product abelian surfaces and their Kummer surfaces.

We construct moduli curves of polarized supersingular K3 surfaces in characteristic 2 with Artin invariant 2. As an application, we detect a ‘jump’ phenomenon in a family of automorphism groups of supersingular K3 surfaces with a constant Néron–Severi lattice.

We show that the bi-Lipschitz equivalence of analytic function germs (${\open C}^{2}$, 0)→(${\open C}$, 0) admits continuous moduli. More precisely, we propose an invariant of the bi-Lipschitz equivalence of such germs that varies continuously in many analytic families ft: (${\open C}^{2}$, 0)→(${\open C}$, 0). For a single germ f the invariant of f is given in terms of the leading coefficients of the asymptotic expansions of f along the branches of generic polar curve of f.

We describe birational models and decide the rationality/unirationality of moduli spaces $\cal A$d (and $\cal A$levd) of (1, d)-polarized Abelian surfaces (with canonical level structure, respectively) for small values of d. The projective lines identified in the rational/unirational moduli spaces correspond to pencils of Abelian surfaces traced on nodal threefolds living naturally in the corresponding ambient projective spaces, and whose small resolutions are new Calabi–Yau threefolds with Euler characteristic zero.

We prove that the moduli space $\cal A$11lev of <$>(1,11)-polarized Abelian surfaces with level structure of canonical type is birational to Klein's cubic hypersurface in P4. Therefore, $\cal A$11lev is unirational but not rational, and there are no Γ11-cusp forms of weight 3. The same methods also provide an easy proof of the rationality of $\cal A$9lev.

This article treats compactifications of the space of generalized spin curves. Generalized spin curves, or r-spin curves, are pairs (X,L) with X a smooth curve and L a line bundle whose rth tensor power is isomorphic to the canonical bundle of X. These are a natural generalization of 2-spin curves (algebraic curves with a theta-characteristic), which have been of interest recently, in part because of their applications to fermionic string theory. Three different compactifications over Z[1/r], all using torsion-free sheaves, are constructed. All three yield algebraic stacks, one of which is shown to have Gorenstein singularities that can be described explicitly, and one of which is smooth. All three compactifications generalize constructions of Deligne and Cornalba done for the case when r=2.