Recently, Brietzke, Silva and Sellers [‘Congruences related to an eighth order mock theta function of Gordon and McIntosh’, J. Math. Anal. Appl.479 (2019), 62–89] studied the number $v_{0}(n)$ of overpartitions of $n$ into odd parts without gaps between the nonoverlined parts, whose generating function is related to the mock theta function $V_{0}(q)$ of order 8. In this paper we first present a short proof of the 3-dissection for the generating function of $v_{0}(2n)$. Then we establish three congruences for $v_{0}(n)$ along certain progressions which are subsequences of the integers $4n+3$.

We investigate the arithmetic properties of the second-order mock theta function $B(q)$ and establish two identities for the coefficients of this function along arithmetic progressions. As applications, we prove several congruences for these coefficients.

In his last letter to Hardy, Ramanujan defined 17 functions 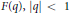$F\left( q \right),\,\left| q \right|\,<\,1$, which he called mock $\theta $-functions. He observed that as 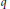$q$ radially approaches any root of unity $\zeta $ at which 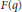$F\left( q \right)$ has an exponential singularity, there is a $\theta $-function 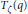${{T}_{\zeta }}\left( q \right)$ with 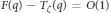$F\left( q \right)\,-\,{{T}_{\zeta }}\left( q \right)\,=\,O\left( 1 \right)$. Since then, other functions have been found that possess this property. These functions are related to a function 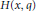$H\left( x,\,q \right)$, where $x$ is usually 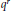${{q}^{r}}$ or 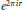${{e}^{2\pi ir}}$ for some rational number $r$. For this reason we refer to 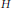$H$ as a “universal” mock $\theta $-function. Modular transformations of 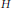$H$ give rise to the functions 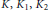$K,\,{{K}_{1}},\,{{K}_{2}}$. The functions 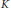$K$ and 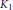${{K}_{1}}$ appear in Ramanujan's lost notebook. We prove various linear relations between these functions using Appell–Lerch sums (also called generalized Lambert series). Some relations (mock theta “conjectures”) involving mock $\theta $-functions of even order and 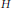$H$ are listed.

In his last letter to Hardy, Ramanujan defined 17 functions $F\left( q \right)$, where $\left| q \right|<1$. He called them mock theta functions, because as $q$ radially approaches any point ${{e}^{2\pi ir}}\left( r\,\text{rational} \right)$, there is a theta function ${{F}_{r}}\left( q \right)$ with $F\left( q \right)-{{F}_{r}}\left( q \right)=O\left( 1 \right)$. In this paper we establish the relationship between two families of mock theta functions.