In this work, we study a high order derivative in time problem. First, we show that there exists a sequence of elements of the spectrum which tends to infinity and therefore, it is ill posed. Then, we prove the uniqueness of solutions for this problem by adapting the logarithmic arguments to this situation. Finally, the results are applied to the backward in time problem for the generalized linear Burgers’ fluid, a couple of heat conduction problems and a viscoelastic model.

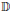For an analytic function $f$ on the unit disk $\mathbb{D}$, we show that the 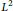${{L}^{2}}$ integral mean of $f$ on 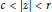$\text{c}\,\text{}\,\text{ }\!\!|\!\!\text{ z }\!\!|\!\!\text{ }\,\text{}\,\text{r}$ with respect to the weighted area measure 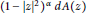${{\left( 1\,-\,|z{{|}^{2}} \right)}^{\alpha }}dA\left( z \right)$ is a logarithmically convex function of $r$ on 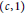$\left( c,\,1 \right)$, where $-3\,\le \,\alpha \,\le \,0\,\text{and}\,\text{c}\,\in \,[\,0,\,1)$. Moreover, the range 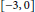$[-3,\,0]$ for $\alpha $ is best possible. When 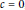$c\,=\,0$, our arguments here also simplify the proof for several results we obtained in earlier papers.

For $0<p<\infty$ and $-2\leq {\it\alpha}\leq 0$ we show that the $L^{p}$ integral mean on $r\mathbb{D}$ of an analytic function in the unit disk $\mathbb{D}$ with respect to the weighted area measure $(1-|z|^{2})^{{\it\alpha}}\,dA(z)$ is a logarithmically convex function of $r$ on $(0,1)$.

Bounds for Hardy differences, that is, improvements and reverses of the well-known Hardy inequality, are obtained.