Assume that $R$ is a commutative Noetherian ring with non-zero identity, $\mathfrak{a}$ is an ideal of $R$, and $X$ is an $R$-module. In this paper, we first study the finiteness of Betti numbers of local cohomology modules $\text{H}_{\mathfrak{a}}^{i}\left( X \right)$. Then we give some inequalities between the Betti numbers of $X$ and those of its local cohomology modules. Finally, we present many upper bounds for the flat dimension of $X$ in terms of the flat dimensions of its local cohomology modules and an upper bound for the flat dimension of $\text{H}_{\mathfrak{a}}^{i}\left( X \right)$ in terms of the flat dimensions of the modules $\text{H}_{\mathfrak{a}}^{j}\left( X \right),j\ne i$, and that of $X$.

Let $\mathfrak{a}$ be an ideal of a commutative Noetherian ring $R$ and $M$ and $N$ two finitely generated $R$-modules. Our main result asserts that if $R/\mathfrak{a}\,\le \,1$, then all generalized local cohomology modules $H_{\mathfrak{a}}^{i}(M,\,N)$ are $\mathfrak{a}$-cofinite.

Let 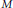$M$ be a finite module over a commutative noetherian ring $R$. For ideals $\mathfrak{a}$ and $\mathfrak{b}$ of $R$, the relations between cohomological dimensions of 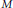$M$ with respect to 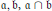$\mathfrak{a},\,\mathfrak{b},\,\mathfrak{a}\,\cap \,\mathfrak{b}$ and 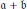$\mathfrak{a}\,+\,\mathfrak{b}$ are studied. When $R$ is local, it is shown that 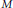$M$ is generalized Cohen–Macaulay if there exists an ideal $\mathfrak{a}$ such that all local cohomology modules of 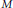$M$ with respect to $\mathfrak{a}$ have finite lengths. Also, when $r$ is an integer such that 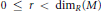$0\,\le \,r\,<\,{{\dim}_{R}}(M)$, any maximal element q of the non-empty set of ideals {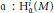$\mathfrak{a}\,:\,\text{H}_{\mathfrak{a}}^{i}(M)$ is not artinian for some $i$, 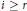$i\,\ge \,r$} is a prime ideal, and all Bass numbers of 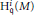$\text{H}_{\mathfrak{q}}^{i}(M)$ are finite for all 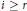$i\,\ge \,r$.

This paper discusses the connection between the local cohomology modules and the Serre classes of $R$-modules. This connection has provided a common language for expressing some results regarding the local cohomology $R$-modules that have appeared in different papers.

The face ring of a homology manifold (without boundary) modulo a generic system of parameters is studied. Its socle is computed and it is verified that a particular quotient of this ring is Gorenstein. This fact is used to prove that the algebraic g-conjecture for spheres implies all enumerative consequences of its far-reaching generalization (due to Kalai) to manifolds. A special case of Kalai’s conjecture is established for homology manifolds that have a codimension-two face whose link contains many vertices.

This paper generalizes, in two senses, work of Petzl and Sharp, who showed that, for a $\mathbb{Z}$-graded module $M$ over a $\mathbb{Z}$-graded commutative Noetherian ring $R$, the graded Cousin complex for $M$ introduced by Goto and Watanabe can be regarded as a subcomplex of the ordinary Cousin complex studied by Sharp, and that the resulting quotient complex is always exact. The generalizations considered in this paper are, firstly, to multigraded situations and, secondly, to Cousin complexes with respect to more general filtrations than the basic ones considered by Petzl and Sharp. New arguments are presented to provide a sufficient condition for the exactness of the quotient complex in this generality, as the arguments of Petzl and Sharp will not work for this situation without additional input.

AMS 2000 Mathematics subject classification: Primary 13A02; 13E05; 13D25; 13D45