Let 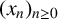$(x_n)_{n\geq 0}$ be a linear recurrence sequence of order $k\geq 2$ satisfying

$$ \begin{align*}x_n=a_1x_{n-1}+a_2x_{n-2}+\dots+a_kx_{n-k}\end{align*} $$

$n\geq k$

$a_1,\dots ,a_k,x_0,\dots , x_{k-1}\in \mathbb {Z},$

$a_k\neq 0$

$(x_n)_{n\geq 0}$

$\mathbb {Q}_p$

$\pm \alpha $

$\alpha $

$\mathbb {Q}_p$

$(x_n)_{n\geq 0}$

$\mathbb {Q}_p$

$\mathbb {Q}$

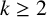Let $(x_n)_{n\geq 0}$ be a linear recurrence of order $k\geq 2$ satisfying 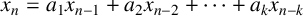$x_n=a_1x_{n-1}+a_2x_{n-2}+\cdots +a_kx_{n-k}$ for all integers 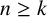$n\geq k$, where 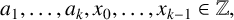$a_1,\ldots ,a_k,x_0,\ldots , x_{k-1}\in \mathbb {Z},$ with 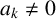$a_k\neq 0$. Sanna [‘The quotient set of k-generalised Fibonacci numbers is dense in 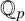$\mathbb {Q}_p$’, Bull. Aust. Math. Soc. 96(1) (2017), 24–29] posed the question of classifying primes p for which the quotient set of 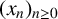$(x_n)_{n\geq 0}$ is dense in $\mathbb {Q}_p$. We find a sufficient condition for denseness of the quotient set of the kth-order linear recurrence 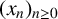$(x_n)_{n\geq 0}$ satisfying 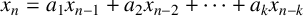$ x_{n}=a_1x_{n-1}+a_2x_{n-2}+\cdots +a_kx_{n-k}$ for all integers 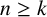$n\geq k$ with initial values $x_0=\cdots =x_{k-2}=0,x_{k-1}=1$, where 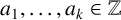$a_1,\ldots ,a_k\in \mathbb {Z}$ and 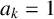$a_k=1$. We show that, given a prime p, there are infinitely many recurrence sequences of order $k\geq 2$ whose quotient sets are not dense in 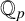$\mathbb {Q}_p$. We also study the quotient sets of linear recurrence sequences with coefficients in certain arithmetic and geometric progressions.

We show that in a parametric family of linear recurrence sequences $a_1(\alpha ) f_1(\alpha )^n + \cdots + a_k(\alpha ) f_k(\alpha )^n$ with the coefficients $a_i$ and characteristic roots $f_i$ , $i=1, \ldots ,k$ , given by rational functions over some number field, for all but a set of elements $\alpha $ of bounded height in the algebraic closure of ${\mathbb Q}$ , the Skolem problem is solvable, and the existence of a zero in such a sequence can be effectively decided. We also discuss several related questions.

Let $X$ be a finite-dimensional connected compact abelian group equipped with the normalized Haar measure $\unicode[STIX]{x1D707}$. We obtain the following mean ergodic theorem over ‘thin’ phase sets. Fix $k\geq 1$ and, for every $n\geq 1$, let $A_{n}$ be a subset of $\mathbb{Z}^{k}\cap [-n,n]^{k}$. Assume that $(A_{n})_{n\geq 1}$ has $\unicode[STIX]{x1D714}(1/n)$ density in the sense that $\lim _{n\rightarrow \infty }(|A_{n}|/n^{k-1})=\infty$. Let $T_{1},\ldots ,T_{k}$ be ergodic automorphisms of $X$. We have

$$\begin{eqnarray}\frac{1}{|A_{n}|}\mathop{\sum }_{(n_{1},\ldots ,n_{k})\in A_{n}}f_{1}(T_{1}^{n_{1}}(x))\cdots f_{k}(T_{k}^{n_{k}}(x))\stackrel{L_{\unicode[STIX]{x1D707}}^{2}}{\longrightarrow }\int f_{1}\,d\unicode[STIX]{x1D707}\cdots \int f_{k}\,d\unicode[STIX]{x1D707},\end{eqnarray}$$

$f_{1},\ldots ,f_{k}\in L_{\unicode[STIX]{x1D707}}^{\infty }$

$T_{i}$

$A_{n}$

$[0,n]^{k}$

$n$

$A_{i}$

We conjecture that bounded generalised polynomial functions cannot be generated by finite automata, except for the trivial case when they are ultimately periodic.

Using methods from ergodic theory, we are able to partially resolve this conjecture, proving that any hypothetical counterexample is periodic away from a very sparse and structured set. In particular, we show that for a polynomial $p(n)$ with at least one irrational coefficient (except for the constant one) and integer $m\geqslant 2$, the sequence $\lfloor p(n)\rfloor \hspace{0.2em}{\rm mod}\hspace{0.2em}m$ is never automatic.

We also prove that the conjecture is equivalent to the claim that the set of powers of an integer $k\geqslant 2$ is not given by a generalised polynomial.

Let K be a number field. For f∈K[x], we give an upper bound on the least positive integer T=T(f) such that no quotient of two distinct Tth powers of roots of f is a root of unity. For each ε>0 and each f∈ℚ[x] of degree d≥d(ε) we prove that . In the opposite direction, we show that the constant 2 cannot be replaced by a number smaller than 1 . These estimates are useful in the study of degenerate and nondegenerate linear recurrence sequences over a number field K.