We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use a special tiling for the hyperbolic d-space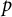 
$\mathbb {H}^d$ for 
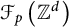$d=2,3,4$ to construct an (almost) explicit isomorphism between the Lipschitz-free space 
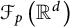$\mathcal {F}(\mathbb {H}^d)$ and 
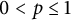$\mathcal {F}(P)\oplus \mathcal {F}(\mathcal {N})$, where P is a polytope in 
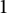$\mathbb {R}^d$ and 
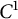$\mathcal {N}$ a net in 
$\mathbb {H}^d$ coming from the tiling. This implies that the spaces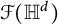 
$\mathcal {F}(\mathbb {H}^d)$ and 
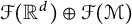$\mathcal {F}(\mathbb {R}^d)\oplus \mathcal {F}(\mathcal {M})$ are isomorphic for every net 
$\mathcal {M}$ in 
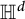$\mathbb {H}^d$. In particular, we obtain that, for 
$d=2,3,4$,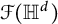 
$\mathcal {F}(\mathbb {H}^d)$ has a Schauder basis. Moreover, using a similar method, we also give an explicit isomorphism between 
$\mathrm {Lip}(\mathbb {H}^d)$ and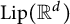 
$\mathrm {Lip}(\mathbb {R}^d)$.
