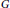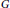Let $G$ be a graph and let $\tau $ be an assignment of nonnegative integer thresholds to the vertices of $G$. A subset of vertices, 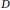$D$, is said to be a $\tau $-dynamicmonopoly if 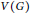$V\left( G \right)$ can be partitioned into subsets 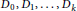${{D}_{0}},\,{{D}_{1}},\,\ldots \,,\,{{D}_{k}}$ such that 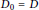${{D}_{0}}\,=\,D$ and for any 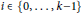$i\,\in \,\left\{ 0,\,\ldots \,,\,k-1 \right\}$, each vertex $v$ in 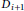${{D}_{i+1}}$ has at least 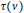$\tau \left( v \right)$ neighbors in ${{D}_{0}}\cup \cdots \cup {{D}_{i}}$. Denote the size of smallest $\tau $-dynamic monopoly by 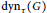$\text{dy}{{\text{n}}_{\tau }}\left( G \right)$ and the average of thresholds in $\tau $ by $\bar{\tau }$. We show that the values of 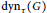$\text{dy}{{\text{n}}_{\tau }}\left( G \right)$ over all assignments $\tau $ with the same average threshold is a continuous set of integers. For any positive number 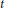$t$, denote the maximum 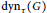$\text{dy}{{\text{n}}_{\tau }}\left( G \right)$ taken over all threshold assignments $\tau $ with 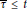$\bar{\tau }\,\le \,t$, by 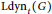$\text{Ldy}{{\text{n}}_{t}}\left( G \right)$. In fact, 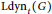$\text{Ldy}{{\text{n}}_{t}}\left( G \right)$ shows the worst-case value of a dynamicmonopoly when the average threshold is a given number 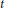$t$. We investigate under what conditions on 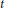$t$, there exists an upper bound for 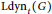$\text{Ldy}{{\text{n}}_{t}}\left( G \right)$ of the form 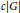$c\left| G \right|$, where 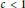$c\,<\,1$. Next, we show that 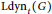$\text{Ldy}{{\text{n}}_{t}}\left( G \right)$ is 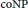$\text{coNP}$-hard for planar graphs but has polynomial-time solution for forests.

Let $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}G$ be a graph and ${{\tau }}$ be an assignment of nonnegative thresholds to the vertices of $G$. A subset of vertices, $D$, is an irreversible dynamic monopoly of $(G, \tau )$ if the vertices of $G$ can be partitioned into subsets $D_0, D_1, \ldots, D_k$ such that $D_0=D$ and, for all $i$ with $0 \leq i \leq k-1$, each vertex $v$ in $D_{i+1}$ has at least $\tau (v)$ neighbours in the union of $D_0, D_1, \ldots, D_i$. Dynamic monopolies model the spread of influence or propagation of opinion in social networks, where the graph $G$ represents the underlying network. The smallest cardinality of any dynamic monopoly of $(G,\tau )$ is denoted by $\mathrm{dyn}_{\tau }(G)$. In this paper we assume that the threshold of each vertex $v$ of the network is a random variable $X_v$ such that $0\leq X_v \leq \deg _G(v)+1$. We obtain sharp bounds on the expectation and the concentration of $\mathrm{dyn}_{\tau }(G)$ around its mean value. We also obtain some lower bounds for the size of dynamic monopolies in terms of the order of graph and expectation of the thresholds.