We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
For smooth functions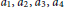 
${{a}_{1}}\,,\,{{a}_{2}}\,,\,{{a}_{3}}\,,\,{{a}_{4}}\,$ on a quaternion Heisenberg group, we characterize the existence of solutions of the partial differential operator system 
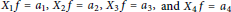${{X}_{1}}f\,=\,{{a}_{1}},\,{{X}_{2}}f=\,{{a}_{2}},\,{{X}_{3}}f\,=\,{{a}_{3}},\,\text{and}\,{{X}_{4}}f\,=\,{{a}_{4}}$. In addition, a formula for the solution function 
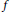$f$ is deduced, assuming solvability of the system.
