We construct some cusped finite-volume hyperbolic n-manifolds 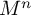 $M^n$ that fibre algebraically in all the dimensions
$M^n$ that fibre algebraically in all the dimensions  $5\leq n \leq 8$. That is, there is a surjective homomorphism
$5\leq n \leq 8$. That is, there is a surjective homomorphism 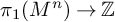 $\pi _1(M^n) \to {\mathbb {Z}}$ with finitely generated kernel. The kernel is also finitely presented in the dimensions
$\pi _1(M^n) \to {\mathbb {Z}}$ with finitely generated kernel. The kernel is also finitely presented in the dimensions 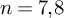 $n=7, 8$, and this leads to the first examples of hyperbolic n-manifolds
$n=7, 8$, and this leads to the first examples of hyperbolic n-manifolds 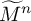 $\widetilde M^n$ whose fundamental group is finitely presented but not of finite type. These n-manifolds
$\widetilde M^n$ whose fundamental group is finitely presented but not of finite type. These n-manifolds 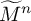 $\widetilde M^n$ have infinitely many cusps of maximal rank and, hence, infinite Betti number
$\widetilde M^n$ have infinitely many cusps of maximal rank and, hence, infinite Betti number 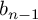 $b_{n-1}$. They cover the finite-volume manifold
$b_{n-1}$. They cover the finite-volume manifold 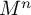 $M^n$. We obtain these examples by assigning some appropriate colours and states to a family of right-angled hyperbolic polytopes
$M^n$. We obtain these examples by assigning some appropriate colours and states to a family of right-angled hyperbolic polytopes  $P^5, \ldots , P^8$, and then applying some arguments of Jankiewicz, Norin and Wise [18] and Bestvina and Brady [7]. We exploit in an essential way the remarkable properties of the Gosset polytopes dual to
$P^5, \ldots , P^8$, and then applying some arguments of Jankiewicz, Norin and Wise [18] and Bestvina and Brady [7]. We exploit in an essential way the remarkable properties of the Gosset polytopes dual to 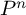 $P^n$, and the algebra of integral octonions for the crucial dimensions
$P^n$, and the algebra of integral octonions for the crucial dimensions  $n=7,8$.
$n=7,8$.