Let 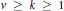 $v\,\ge \,k\,\ge \,1$ and
$v\,\ge \,k\,\ge \,1$ and 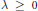 $\lambda \,\ge \,0$ be integers. A block design
$\lambda \,\ge \,0$ be integers. A block design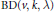 $\text{BD}\left( v,\,k,\,\lambda \right)$ is a collection
$\text{BD}\left( v,\,k,\,\lambda \right)$ is a collection 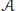 $\mathcal{A}$ of
$\mathcal{A}$ of  $k$-subsets of a
$k$-subsets of a  $v$-set
$v$-set 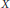 $X$ in which every unordered pair of elements from
$X$ in which every unordered pair of elements from 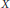 $X$ is contained in exactly
$X$ is contained in exactly  $\lambda $ elements of
$\lambda $ elements of 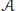 $\mathcal{A}$. More generally, for a fixed simple graph
$\mathcal{A}$. More generally, for a fixed simple graph  $G$, a graph design
$G$, a graph design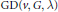 $\text{GD}\left( v,\,G,\,\lambda \right)$ is a collection
$\text{GD}\left( v,\,G,\,\lambda \right)$ is a collection 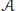 $\mathcal{A}$ of graphs isomorphic to
$\mathcal{A}$ of graphs isomorphic to  $G$ with vertices in
$G$ with vertices in 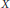 $X$ such that every unordered pair of elements from
$X$ such that every unordered pair of elements from 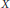 $X$ is an edge of exactly
$X$ is an edge of exactly  $\lambda $ elements of
$\lambda $ elements of 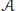 $\mathcal{A}$. A famous result of Wilson says that for a fixed
$\mathcal{A}$. A famous result of Wilson says that for a fixed  $ $ and
$ $ and  $\lambda $, there exists a
$\lambda $, there exists a 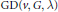 $\text{GD}\left( v,\,G,\,\lambda \right)$ for all sufficiently large
$\text{GD}\left( v,\,G,\,\lambda \right)$ for all sufficiently large  $ $ satisfying certain necessary conditions. A block (graph) design as above is resolvable if
$ $ satisfying certain necessary conditions. A block (graph) design as above is resolvable if 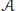 $\mathcal{A}$ can be partitioned into partitions of (graphs whose vertex sets partition)
$\mathcal{A}$ can be partitioned into partitions of (graphs whose vertex sets partition) 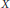 $X$. Lu has shown asymptotic existence in
$X$. Lu has shown asymptotic existence in  $v$ of resolvable
$v$ of resolvable 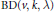 $\text{BD}\left( v,\,k,\,\lambda \right)$, yet for over twenty years the analogous problem for resolvable
$\text{BD}\left( v,\,k,\,\lambda \right)$, yet for over twenty years the analogous problem for resolvable 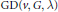 $\text{GD}\left( v,\,G,\,\lambda \right)$ has remained open. In this paper, we settle asymptotic existence of resolvable graph designs.
$\text{GD}\left( v,\,G,\,\lambda \right)$ has remained open. In this paper, we settle asymptotic existence of resolvable graph designs.