We show that every orbispace satisfying certain mild hypotheses has ‘enough’ vector bundles. It follows that the 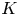 $K$-theory of finite rank vector bundles on such orbispaces is a cohomology theory. Global presentation results for smooth orbifolds and derived smooth orbifolds also follow.
$K$-theory of finite rank vector bundles on such orbispaces is a cohomology theory. Global presentation results for smooth orbifolds and derived smooth orbifolds also follow.