In this work we study the Cauchy problem in Gevrey spaces for a generalized class of equations that contains the case $b=0$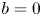 of the $b$
of the $b$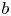 -equation. For the generalized equation, we prove that it is locally well-posed for initial data in Gevrey spaces. Moreover, as we move to global well-posedness, we show that for a particular choice of the parameter in the equation the local solution is global analytic in both time and spatial variables.
-equation. For the generalized equation, we prove that it is locally well-posed for initial data in Gevrey spaces. Moreover, as we move to global well-posedness, we show that for a particular choice of the parameter in the equation the local solution is global analytic in both time and spatial variables.